2.3. Теорема о трёх синусах

Дано: двугранный угол,

АКО – линейный угол двугранного

угла (АОτ_2, ОККВ, АК), АКО= α;

АВ – прямая: АВ τ₁, АВК=β,

АBО – угол, который составляет АВ

с гранью τ₂, АВО=γ;

Доказать: sin γ = sin α ∙ sin β

Доказательство

1. Пусть АВ=х.

2. АВК – прямоугольный, АК= .

3. АОК – прямоугольный, АО= , учитывая (2) АО= .

4. АОВ – прямоугольный, АО=xsinγ

5. Из (3) и (4) xsinγ= , sinγ= .

2. 4. Теорема косинусов для трёхгранного угла

Д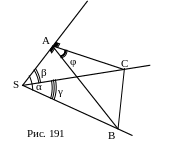 ано: SABC – трёхгранный угол,

.

ВАС – линейный угол двугранного угла,

противолежащего плоскому углу BSC,

равному γ.

Доказать:

Доказательство.

1. Пусть SA=х.

Тогда в треугольнике ASB .

В треугольнике ASC .

2. По теореме косинусов для треугольника АВС

, .

3. По теореме косинусов для треугольника ВSС

,

4. Из (2) и (3) получим равенство

,

,

,

,

,

, .

3. Задачи к теоретической карте №3

3.1. Угол между прямой и плоскостью

№1 (устно). На рисунке 192 изображён прямоугольный параллелепипед. Занумерованные углы запишите как углы между прямой и плоскостью.

№2. ABCDA₁B₁C₁D₁ – куб. Вычислить углы, которые образуют:

1) DC₁ c плоскостями граней куба (устно);

Обозначим угол, образованный данной

прямой с гранью ABCD (A ₁B₁C₁D₁) α, с

гранью АА₁В₁В (DD₁C₁C) β, с гранью

АА₁D₁D (BB₁C₁C) γ.

Ответ: α =45, β=0,γ=45.

2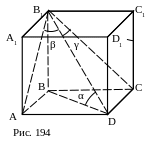 ) DВ₁ c плоскостями граней куба (устно);

Воспользуемся обозначениями пункта (1).

Ответ: α =β=γ=arctg .

3)A₁D с плоскостью АВ₁С ₁;

План решения.

1. А₁О  АВ₁С ₁,

OD– проекция A₁D на плоскость АВ₁С₁.

А₁DO=α – искомый.

2. А₁DO – прямоугольный.

3. А₁О, A₁D выразить через ребро куба.

4. sinα.

Ответ: 30.

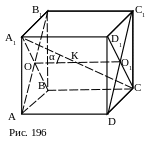
4) A₁С с плоскостью АВ₁С ₁;

План решения

1. А₁О  АВ₁С ₁, СО₁ АВ₁С ₁,

OО₁– проекция A₁С на плоскость АВ₁С ₁.

А₁КO = α – искомый.

2. А₁КO – прямоугольный.

3. А₁О, ОК выразить через ребро куба.

4. tg α.

Ответ: arctg .

5) A₁D с плоскостью ВС ₁D;

План решения

1. А₁С  ВС₁D, OD – проекция A₁D на

плоскость ВС₁D;

А₁DO = α – искомый.

2. А₁DO – прямоугольный.

3. А₁D, ОD выразить через ребро куба.

4. cos α.

Ответ: arccos .

6) В₁D с плоскостью ВС₁D;

План решения

1. А₁С  ВС₁D, РО  ВС₁D,

где Р – точка пересечения А₁С и В₁D;

OD – проекция В₁D на плоскость ВС₁D;

РDO = α – искомый.

2. РDO – прямоугольный.

3. РD, ОD выразить через ребро куба. 4. cos α. Ответ: arccos .

7) В₁С с плоскостью ВС₁D;

План решения

1. А₁С  ВС₁D, OР – проекция В₁С на

плоскость ВС ₁D;

СРО = α – искомый.

Рис. 199

2. DPС – прямоугольный.

3. РС, DC выразить через ребро куба.

4. tg α.

Ответ: arctg .

Замечание. Можно рассмотреть ОPС, выразить через ребро куба ОР и РС и найти cos α. Тогда α = .

№ 3. РАВС – правильный тетраэдр. Вычислить угол φ, который составляют:

1 ) ребро с плоскостью грани, в которой оно не лежит;

План решения.

Рассмотреть ребро АР и плоскость грани АВС.

1. РОАВС; АР– наклонная, АО – проекция,

РАО=φ.

2. Выразить АО через ребро пирамиды а.

3. cos φ.

Ответ: .

Все другие рёбра образуют с гранями тетраэдра такие же углы.

2 ) апофема боковой грани с плоскостью

основания;

План решения.

Рассмотреть апофему РК.

1. РОАВС; РК – наклонная, ОК – проекция, РКО=φ.

2. Выразить ОК и РК через ребро тетраэдра а.

3. cos φ Ответ: .

3) высота пирамиды с плоскостью

боковой грани;

План решения.

Рассмотреть высоту РО.

1. ОFРК, ОFСРВ.

2. ОР – наклонная, PF – проекция,

ОРF=φ=ОРК.

3. Выразить ОК и РК через ребро

тетраэдра а.

4. sin φ. Ответ: .

№4. Отрезок длиной 20 см пересекает плоскость. Концы его находятся на расстоянии 6 см и 4 см от плоскости. Найти угол между данным отрезком и плоскостью.

План решения.

1. АА₁ОВВ₁О.

2. АО.

3. sin AOA₁.

Ответ: 30.

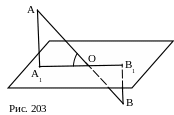
№ 5. Отрезок АВ имеет длину 1 и упирается концами в две перпендикулярные плоскости α и β, причём Аα, Вβ. Прямая АВ образует с плоскостью α угол φ_1, а с плоскостью β угол φ₂. Найти длины проекций отрезка АВ на каждую из плоскостей и на прямую их пересечения.

План решения.

1. Построения: АО₁l, BО₂l.

2. АО₁β, ВО₂α.

3. ВО₁ (АВО₁).

4. АО₂ (АВО₂).

5. АО₁ (АВО₁), АО₂ (АВО₂).

6.О₁О₂.

Ответ: .

№6. Измерения прямоугольного параллелепипеда 3 см, 4 см, 5 см. Найти углы, образуемые его диагоналями с гранями.

План решения.

1. α – угол, образованный диагональю В₁D

с гранью ABCD.

β– угол, образованный диагональю В₁D

с гранью AA₁B₁B.

γ– угол, образованный диагональю В₁D

с гранью BB₁CC₁.

2. B₁D.

3.sin α. 4. sin β. 5. sin γ.

Ответ: 45, , .

№7. Определить объём прямоугольного параллелепипеда, диагональ которого равна l и составляет с одной гранью угол 30, а с другой 45.

П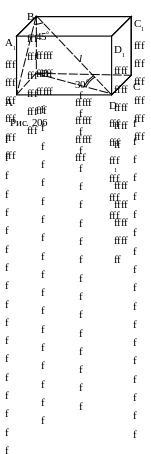 лан решения.

1. В₁DB=30, АВ₁D=45.

2. ВВ₁, BD.

3. АD.

4. AB.

5. V .

Ответ: .

№8. Основание прямого параллелепипеда - ромб со стороной 3 см; диагонали параллелепипеда образуют с основанием углы в 30 и 45. Найти высоту параллелепипеда и углы ромба.

План решения.

Пусть высота параллелепипеда равна h.

1. Выразить BD и ОD через h.

2. Выразить АС и АО через h.

3. Составить и решить относительно h

уравнение (AOD).

4. АО, OD.

5. cos OAD, cosODA (или синус, или

тангенс).

6. OAD, ODA.

7. ВAD, СDA.

Ответ: 3 см, 60, 120.

№9. Рёбра прямоугольного параллелепипеда относятся как 3:4:12. Через большее ребро проведено диагональное сечение. Найти синус угла между плоскостью этого сечения и не лежащей в ней диагональю параллелепипеда.

П лан решения.

1. Построения:

В₁М  А₁ С₁, В₁М  АА₁ С₁С,

DN  AC, DN  АА₁ С₁С,

MN – проекция B₁D на АА₁ С₁С.

 - искомый.

2. Пусть х – общая мера измерений

параллелепипеда.

Выразить В₁М, B₁О через х.

3. sin  ( ОB₁M).

Ответ:

№10. В правильной треугольной призме АВСА₁В₁С₁, боковое ребро которой равно стороне основания, найти угол между диагональю АВ₁ и плоскостью АА₁С₁С.

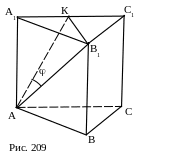
План решения.

1.Построения: В₁КА₁С₁, АК.

2. К –середина А₁С₁, В₁К АА₁С₁С.

3. В₁К.

4. АВ₁.

5. sin.

Ответ: .

№11. Высота прямой призмы АВСА₁В₁С₁ равна 12. Основание призмы  АВС, в котором АВ=АС, ВС=18, tgC=0,4. Найти тангенс угла между прямой АС₁ и плоскостью ВВ₁С₁.

П лан решения.

1. Построения: АРСВ. АР ВВ₁С₁.

 - искомый.

2. РС.

3. tg C, AP.

4. C₁P.

5.tg .

Ответ: 0,24.

Рис. 210

№12. ABCD – квадрат, СМ – перпендикуляр к плоскости квадрата. Определить угол наклона прямой МВ к плоскости МАС.

План решения.

1. АМСABCD, ВОАС: ВОАМС.

2. МО  проекция ВМ на АМС.

3. ВМО – искомый.

Ответ: ВМО.

№13. ABC – треугольник, О – центр окружности, описанной около треугольника ABC. OS – перпендикуляр к плоскости треугольника. Определить угол наклона SO к плоскости АSC.

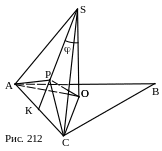
План решения.

1. Построения: ОРASC, SP, SK, AP,

CP, OP,OC.

2. SP – проекция SO на плоскостьASC.

3. SA=SC (равные наклонные равных

проекций). ASCравнобедренный.

4. AP=CP (равные проекции равных наклонных).

5. Точка Р принадлежит серединному перпендикуляру к отрезку АС, то есть

высоте SK в треугольникеASC.

Вывод: угол наклона SO к плоскости АSC  =OSK.

Замечание. Рассуждения не изменятся, если в условии задачи 13 заменить треугольник на любой многоугольник, около которого можно описать окружность (прямоугольник, в частности , квадрат, равнобокую трапецию и другие).

№14. Высота правильной четырёхугольной пирамиды равна h и составляет угол φ с плоскостью боковой грани. Найти полную поверхность пирамиды.

План решения.

1. OSP= (задача 10).

2. ОР, SP.

3. AD.

4. S_{полной поверхности}.

Ответ:

№ 15. Основанием пирамиды SABCD является квадрат ABCD. Точка М делит отрезок АВ в отношении 3:1, считая от точки А, прямая SM перпендикулярна плоскости основания. Найти тангенс угла между ребром SC и плоскостью основания, если ребро SD образует с плоскостью основания угол α.

План решения.

Пусть сторона основания равна а.

1.Выразить MD через а.

2. Выразить SM через а.

3. Выразить МС через а.

4.tgSCM.

Ответ:

№ 16. В правильной треугольной пирамиде SABC с основанием АВС известны рёбра: АВ= , SC=17. Найти угол, образованный плоскостью основания и прямой АМ, где М точка пересечения медиан грани SBC.

План решения.

1. Построения.

1.1. SO  ABC.

1.2. MF || SO.

1.3. MAF искомый.

2. AD. 3. OD. 4. DF. 5. AF.

6. OC. 7. SO. 8. MF. 9. tgMAF.

Ответ: .

№17. В треугольной пирамиде РАВС построено сечение АМK, площадь которого равна S. Ребро АР равно 3 и составляет с плоскостью сечения угол α. Найти объём пирамиды РАКМ.

План решения.

1. Высота пирамиды РO. (Без построения

ясно, что РО = АРsin α).

2. V_РAВC.

Ответ: Ssinα.