Свойства коэффициента корреляции

Коэффициент корреляции обладает свойствами:

1) если и независимы, то ;

2) всегда ;

3) тогда и только тогда, когда и п. н. линейно связаны, т.е. существуют числа и такие, что .

4) Говорят, что и отрицательно коррелированы, если , положительно коррелированы, если , инекоррелированы, если .

5) Для любых случайных величин и с конечной и ненулевой дисперсией при любых постоянных и имеет место равенство:

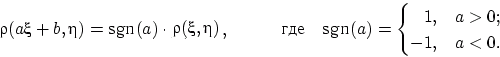
Регрессионный анализ на основе комбинационной группировки

Комбинационные группировки выполнятся по нескольким признакам последовательно. Последовательность устанавливается исходя из логики взаимосвязи показателей. Как правило, группировку начинают с атрибутивного признака. При комбинационной группировке совокупность логически последовательно разбивается на однородные части по отдельным признакам: на группы - по одному признаку, затем внутри каждой группы по второму признаку - на подгруппы и т.д.

Такие группировки предназначены для более глубокого анализа изучаемого явления, позволяют выявить и сравнить различия и связи между исследуемыми признаками, которые невозможно установить на основе изолированных группировок по каждому из исследуемых признаков. Однако следует иметь в виду, что при изучении влияния большого числа признаков применение комбинационных группировок невозможно, так как это приводит к дроблению информации, а значит, к затушевыванию проявлений закономерности. Даже при наличии больших объемов информации приходится ограничиваться двумя – четырьмя признаками.

Комбинационная группировка по двум признакам (X, Y) оформляется в виде шахматной таблицы, в которой значения одного признака X откладываются по строкам, а значения второго признака Y – по столбцам. На пересечении j–ого столбца и i-ой строки (в теле таблицы) находятся частоты совместного проявления значения признака Y в j-ом столбце и значения признака X в i -ой строке.

Оценка существенности параметров линейной регрессии и корреляции. F-критерий Фишера. Дисперсионный анализ

После построения уравнения линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, следовательно, фактор х не оказывает влияния на результат у.

Величина F–отношения (F-критерий) получается при сопоставлении факторной и остаточной дисперсии в расчете на одну степень свободы.

F = D_факт / D_ост (5)

F-критерий проверки для нулевой гипотезы Н₀: D_факт = D_ост

Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н₀ необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным (отличным от 1), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: F_факт > F_табл Н₀ отклоняется.

Если же величина оказалась меньше табличной F_факт < F_табл, то вероятность нулевой гипотезы меньше заданного уровня (например, 0, 05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым и не отклоняется. Проверка значимости уравнения регрессии производится на основе дисперсионного анализа. В математической статистике дисперсионный анализ рассмотрен как самостоятельный инструмент (метод) статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества модели. Центральное место в анализе дисперсии занимает разложение общей суммы квадратов отклонений переменной у от среднего значения у на 2 части - «объясненную» и «необъясненную»:

Общая сумма квадратов отклонений

=

Сумма квадратов отклонений, объясненная регрессией

+

Остаточная сумма квадратов отклонений

или Q = Q_R + Q_e (7)

В переводной литературе принято следующее обозначение: TSS = RSS + ESS

- общая сумма квадратов отклонений; (8)

– сумма квадратов отклонений, обусловленная регрессией; (9)

Q = ESS = – остаточная сумма квадратов отклонений. (10)

Таблица: схема дисперсионного анализа.

Средние квадраты и s_R² представляют собой несмещенные оценки зависимой переменной, обусловленных соответственно регрессией или объясняющей переменной х и воздействием неучтенных случайных факторов и ошибок; m – число оцениваемых параметров регрессии, n – число наблюдений. При отсутствии линейной зависимости между зависимой и объясняющей(ими) переменной случайные величины и s_R² имеют ² – распределение соответственно с m-1 и n-m степенями свободы, а их отношение F – распределение с теми же степенями свободы. Поэтому, уравнение регрессии значимо на уровне , если фактически наблюдаемое значение статистики

(11),

где - табличное значение F – критерия Фишера – Снедекора, определенное на уровне значимости при k1 = m-1 и k2 = n-m степенях свободы.

Учитывая смысл величин и s_R², можно сказать, что значение F показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с ее средней.

В случае парной линейной регрессии m = 2, и уравнение регрессии значимо на уровне , если

(12)

В ряде прикладных задач требуется оценить значимость коэффициента корреляции r. При этом исходят из того, что при отсутствии корреляционной связи статистика t, найденная по формуле (4) ( ) имеет t-распределение Стьюдента с (n-2) степенями свободы.

Коэффициент корреляции r_xy значим на уровне , (иначе – гипотеза Н₀ о равенстве генерального коэффициента корреляции нулю отвергается), если

(13),

где -табличное значение t-критерия Стьюдента, определенное на уровне значимости a при числе степеней свободы (n-2).

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка. Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии; вычисляется значение t-критерия, его величина сравнивается с табличным значением при (n-2) степенях свободы. Проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.