
- •Конспект лекций по статистике
- •§5. Сезонные колебания, сезонные индексы и полное разложение дисперсии уровней динамического ряда 99
- •Глава 1. Статистика как наука
- •§1. Происхождение термина «статистика», его значение, особенности.
- •§2. Метод статистики
- •§3. Отрасли статистических наук
- •§4. Общая теория статистики как отрасль статистической науки.
- •§5. Статистический признак. Классификация.
- •§6. Понятие статистической закономерности.
- •Глава 2. Сбор статистической информации (теория статистического наблюдения)
- •§1. Понятие о статистическом наблюдении, этапы его проведения
- •§2. Программно-методологические вопросы статистического наблюдения
- •§3. Важнейшие организационные вопросы статистического наблюдения
- •§4. Основные организационные формы, виды и способы статистического наблюдения
- •§5. Точность наблюдения
- •Глава 3. Статистическая сводка и группировка §1. Задачи сводки и ее содержание
- •§2. Метод группировки и его место в системе статистических методов
- •§3. Виды статистических группировок
- •§4. Принципы построения статистических группировок и классификаций
- •§5. Ряды распределения и группировки
- •§5.1. Огива
- •§6. Сравнимость статистических группировок
- •§7. Метод группировок и многомерные классификации
- •§8. Группировки и классификации в практике статистики
- •Глава 4. Статистические таблицы §1. Элементы статистической таблицы
- •§2. Виды таблиц по подлежащему
- •§3. Виды таблиц по сказуемому
- •§4. Правила при построении таблиц
- •§5. Чтение и анализ таблицы
- •§6. Таблицы и матрицы
- •Глава 5. Статистические показатели
- •§1. Понятие, формы выражения и виды статистических показателей
- •§2. Абсолютные показатели
- •§3. Относительные показатели
- •§4. Средние показатели
- •Глава 6. Аналитическая статистика
- •§1. Структурные средние
- •1) Определение структурных средних в дискретных вариационных рядах
- •2) Определение структурных средних в интервальных вариационных рядах.
- •§2. Дисперсия
- •§4. Показатели вариации
- •§5. Относительные показатели вариации.
- •Глава 7. Корреляционно-регрессионный анализ
- •Изучение степени тесноты между двумя качественными признаками.
- •Глава 8. Выборочное наблюдение
- •Глава 9. Ряды динамики
- •Глава 10. Экономические индексы
- •§1. Понятие экономических индексов. Классификация индексов
- •§2. Индивидуальные и общие индексы
- •§3. Средние экономические индексы.
- •§4. Индексы средних величин.
- •Анализ взаимосвязей
- •Свойства коэффициента корреляции
- •Регрессионный анализ на основе комбинационной группировки
- •Оценка существенности параметров линейной регрессии и корреляции. F-критерий Фишера. Дисперсионный анализ
- •Ряды динамики Интерполяция и экстраполяция (прогнозирование) уровней ряда динамики
- •Экономические индексы
- •§1. Синтетическая и аналитическая концепции индексов
- •§2. Выбор базы и весов индексов
- •§3. Индексы пространственно-территориального сопоставления.
- •§4. Индексы Ласпейреса, Пааше, идеальный индекс Фишера
- •§5. Сезонные колебания, сезонные индексы и полное разложение дисперсии уровней динамического ряда
Глава 9. Ряды динамики
Одной из задач статистики является изучение изменения социально-экономических явлений и процессов во времени. Эта задача решается с помощью составления и анализа рядов динамики.
Ряд динамики представляет собой последовательность числовых значений изучаемого статистического показателя за определенные периоды времени. Числовые значения, составляющие ряд динамики называются уровнями ряда и обозначаются yi (i=1,2,…,n). В зависимости от вида показателей, составляющих ряд динамики, различают ряды абсолютных, относительных и средних величин. Уровни ряда динамики могут относиться к определенным моментам или периодам времени. В зависимости от этого ряды динамики подразделяются на моментные и интервальные.
Моментным называют ряд динамики, уровни которого характеризуют величину изучаемого показателя на определенный момент времени (на конкретную дату). Например: приводится численность населения Российской Федерации (млн. чел.): на 01.01.1999 – 146,3; на 01.01.2000 – 145,6; на 01.01.2001 – 144,8; на 01.01.2002 – 144,0; на 01.01.2003 -145,2.
Интервальным называют ряд динамики, уровни которого характеризуют величину изучаемого показателя за определенный период времени. Например: приводится объем кредитных вложений в экономику страны: 2000 г. – 808; 2001 г. – 1286; 2002 г. – 1755.
Расчет среднего уровня в рядах динамики.
Различают: y1 - начальный уровень ряда, yn – конечный уровень ряда, - средний уровень ряда. В моментном ряду динамики возможны следующие варианты расчета среднего уровня:
Если приводятся данные только на начало и на конец изучаемого периода, то средний уровень рассчитывается, как средняя арифметическая величина из этих двух значений.
Если моменты времени, к которым относятся уровни ряда расположены через равные промежутки, то средний уровень определяется по формуле простой хронологической средней:
 ,
где n
– число уровней ряда.
,
где n
– число уровней ряда.
Если моменты времени, к которым относятся уровни ряда расположены через не равные промежутки, то средний уровень рассчитывается по формуле хронологической взвешенной:
 ,
где
,
где
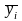 - полусумма двух соседних уровней ряда;
- полусумма двух соседних уровней ряда;
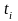 - промежуток между двумя соседними
уровнями ряда, выраженный в днях, месяцах
и т. д. в зависимости от исходных данных.
- промежуток между двумя соседними
уровнями ряда, выраженный в днях, месяцах
и т. д. в зависимости от исходных данных.
В интервальном ряду динамики средний уровень рассчитывается следующим образом:
1.
В ряду с равноотстоящими интервалами
по формуле
простой арифметической средней:
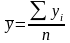 .
.
2. В ряду с не равноотстоящими интервалами по формуле средней арифметической
взвешенной:
 .
.
Основные аналитические и средние показатели рядов динамики.
Кроме среднего уровня для анализа рядов динамики вычисляют следующие аналитические показатели:
Абсолютный прирост (
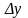 )
)Коэффициент роста (Кр)
Темп роста (Тр)
Темп прироста (Тпр)
Абсолютное значение 1% прироста (Аi)
Возможны 2 варианта сравнения уровней рядов динамики. При 1-ом варианте сравнения каждый i-ый уровень ряда сравнивают с каким-то первым уровнем, выбранным в качестве базы сравнения. Как правило, в качестве базы сравнения выбирают уровень начального периода. Полученные в результате сравнения показатели называются базисными и характеризуют изменение изучаемого показателя в данном периоде, по сравнению с начальным периодом. При втором варианте сравнения каждый i-ый уровень ряда сравнивают с предшествующим уровнем, т. е. база сравнения все время меняется. Рассчитанные при этом варианте показатели называются цепными и характеризуют изменение изучаемого показателя в данном периоде по сравнению с предшествующим.
1) Абсолютный прирост показывает на сколько единиц изменится уровень данного периода, по сравнению с уровнем, выбранным в качестве базы сравнения.
Базисные
показатели:
 ;
цепные показатели:
;
цепные показатели:
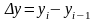 .
.
2) Коэффициент роста показывает, во сколько раз изменился уровень данного периода по сравнению с уровнем, выбранным в качестве базы сравнения.
 (б.)
(б.)
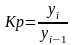 (ц.)
(ц.)
3) Темп роста представляет собой коэффициент роста, выраженный в процентах (%):
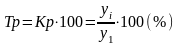 (б.)
(б.)
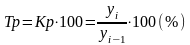 (ц.)
(ц.)
4) Темп прироста характеризует относительное изменение уровней ряда, выраженное в %:
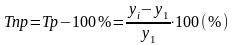 (б.)
(б.)
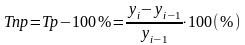 (ц.)
(ц.)
5)
Абсолютное
значение 1% прироста
показывает на сколько единиц изменился
уровень ряда динамики при его изменении
на 1%:
 .
.
Кроме перечисленных аналитических показателей вычисляют средние показатели динамики за определенный период времени. Вычисляют:
1)
среднегодовой
абсолютный прирост,
который показывает на сколько единиц
изменялись уровни ряда динамики ежегодно,
в течение определенного периода времени:
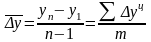 ,
где m
– число цепных абсолютных приростов.
,
где m
– число цепных абсолютных приростов.
2) среднегодовой коэффициент роста, который показывает, во сколько раз ежегодно изменялись уровни ряда динамики в течение определенного периода времени:
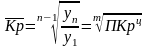
3)
среднегодовой темп роста
представляет собой среднегодовой
коэффициент роста, выраженный в процентах
(%):
 .
.
среднегодовой темп прироста показывает на сколько процентов ежегодно изменялись уровни ряда динамики в течение определенного периода времени:
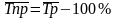 .
.
При сравнении двух и более рядов динамики возникает проблема несопоставимости уровней ряда по следующим причинам: 1) изменение территориальных границ, в пределах которых рассчитываются показатели; 2) изменение уровня цен при расчете показателей; 3) изменение методологии расчета покупателей.
Для привидения таких рядов динамики к сопоставимому виду применяют метод смыкания рядов динамики. Он заключается в том, что для периода, в котором произошли определенные изменения, в расчете показателей рассчитывают коэффициент соотношения уровней и затем все последующие (предшествующие), уровни рядов динамики корректируют с учетом этого коэффициента. При изучении рядов динамики важной задачей является выявление основной тенденции изменения уровней рядов динамики. Для этого используют следующие методы:
1)
Метод
скользящей средней,
который заключается в том, что по исходным
данным для каждого звена по формуле
простой арифметической средней
рассчитываются теоретические уровни,
в которых исключены случайные колебания
уровней рядов динамики. Полученные
теоретические уровни присваивают
периоду, который находится в середине
каждого звена. Например,
трехзвенную скользящую среднюю
рассчитывают следующим образом:
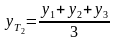 ;
;
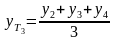 ;
;
 ,
и т. д.
,
и т. д.
2) Метод укрупнения интервалов состоит в том, что первоначальный ряд динамики преобразуется в ряд с более продолжительными периодами времени. Например: месячные уровни товарооборота преобразуют в квартальные уровни.
3) Метод механического выравнивания заключается в том, что на основе рассчитанного среднегодового абсолютного прироста вычисляются теоретические уровни ряда динамики.
4)
Метод
аналитического выравнивания
состоит в том, что на основе математической
функции, которая наиболее точно отражает
основную тенденцию изменения уровней
ряда динамики, строится теоретическая
функция: y(t)=f(t),
где t
– параметр времени. При подборе
математической функции необходимо
свести к минимуму сумму квадратов
отклонений фактических уровней ряда
от теоретических:
 .
Рассмотрим аналитическое
выравнивание ряда динамики по линейной
функции
.
Рассмотрим аналитическое
выравнивание ряда динамики по линейной
функции
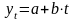 , где t
– параметр времени; a
и b
– параметры линейной функции. Для
определения параметров линейной функции
a
и b
составляют систему уравнений:
, где t
– параметр времени; a
и b
– параметры линейной функции. Для
определения параметров линейной функции
a
и b
составляют систему уравнений:
 .
.
5) Метод интерполяции заключается в том, что на основе выявленных закономерностей изменения уровней ряда динамики рассчитываются неизвестные уровни внутри этого ряда динамики.
6) Метод экстраполяции состоит в том, что на основе выявленной закономерности в изменении уровней ряда строится прогноз на перспективный период времени. Для этого используются следующие формулы:

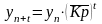
Где
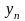 - конечный уровень ряда; t
– срок прогноза;
- конечный уровень ряда; t
– срок прогноза;
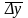 -
среднегодовой абсолютный прирост за
изучаемый период времени;
-
среднегодовой абсолютный прирост за
изучаемый период времени;
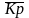 -
среднегодовой коэффициент роста за
изучаемый период времени;
-
среднегодовой коэффициент роста за
изучаемый период времени;
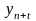 -
перспективное значение уровня цен ряда
динамики.
-
перспективное значение уровня цен ряда
динамики.
