
- •Конспект лекций по статистике
- •§5. Сезонные колебания, сезонные индексы и полное разложение дисперсии уровней динамического ряда 99
- •Глава 1. Статистика как наука
- •§1. Происхождение термина «статистика», его значение, особенности.
- •§2. Метод статистики
- •§3. Отрасли статистических наук
- •§4. Общая теория статистики как отрасль статистической науки.
- •§5. Статистический признак. Классификация.
- •§6. Понятие статистической закономерности.
- •Глава 2. Сбор статистической информации (теория статистического наблюдения)
- •§1. Понятие о статистическом наблюдении, этапы его проведения
- •§2. Программно-методологические вопросы статистического наблюдения
- •§3. Важнейшие организационные вопросы статистического наблюдения
- •§4. Основные организационные формы, виды и способы статистического наблюдения
- •§5. Точность наблюдения
- •Глава 3. Статистическая сводка и группировка §1. Задачи сводки и ее содержание
- •§2. Метод группировки и его место в системе статистических методов
- •§3. Виды статистических группировок
- •§4. Принципы построения статистических группировок и классификаций
- •§5. Ряды распределения и группировки
- •§5.1. Огива
- •§6. Сравнимость статистических группировок
- •§7. Метод группировок и многомерные классификации
- •§8. Группировки и классификации в практике статистики
- •Глава 4. Статистические таблицы §1. Элементы статистической таблицы
- •§2. Виды таблиц по подлежащему
- •§3. Виды таблиц по сказуемому
- •§4. Правила при построении таблиц
- •§5. Чтение и анализ таблицы
- •§6. Таблицы и матрицы
- •Глава 5. Статистические показатели
- •§1. Понятие, формы выражения и виды статистических показателей
- •§2. Абсолютные показатели
- •§3. Относительные показатели
- •§4. Средние показатели
- •Глава 6. Аналитическая статистика
- •§1. Структурные средние
- •1) Определение структурных средних в дискретных вариационных рядах
- •2) Определение структурных средних в интервальных вариационных рядах.
- •§2. Дисперсия
- •§4. Показатели вариации
- •§5. Относительные показатели вариации.
- •Глава 7. Корреляционно-регрессионный анализ
- •Изучение степени тесноты между двумя качественными признаками.
- •Глава 8. Выборочное наблюдение
- •Глава 9. Ряды динамики
- •Глава 10. Экономические индексы
- •§1. Понятие экономических индексов. Классификация индексов
- •§2. Индивидуальные и общие индексы
- •§3. Средние экономические индексы.
- •§4. Индексы средних величин.
- •Анализ взаимосвязей
- •Свойства коэффициента корреляции
- •Регрессионный анализ на основе комбинационной группировки
- •Оценка существенности параметров линейной регрессии и корреляции. F-критерий Фишера. Дисперсионный анализ
- •Ряды динамики Интерполяция и экстраполяция (прогнозирование) уровней ряда динамики
- •Экономические индексы
- •§1. Синтетическая и аналитическая концепции индексов
- •§2. Выбор базы и весов индексов
- •§3. Индексы пространственно-территориального сопоставления.
- •§4. Индексы Ласпейреса, Пааше, идеальный индекс Фишера
- •§5. Сезонные колебания, сезонные индексы и полное разложение дисперсии уровней динамического ряда
Изучение степени тесноты между двумя качественными признаками.
Для определения степени тесноты связи между двумя качественными признаками вычисляют коэффициенты ассоциации и контингенции по формулам:
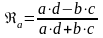 ;
;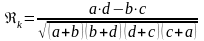 .
.
Для вычисления этих коэффициентов строится таблица сопряженности, которая характеризует связь между двумя качественными признаками, каждый из которых является альтернативным.
-
a
b
a+b
c
d
c+d
a+c
b+d
a+b+c+d
Пример: Определить степень тесноты связи между успешной сдачей экзамена по статистике и посещаемостью занятий по этой же дисциплине:
Группы Студентов Число студентов (чел.) |
Из них: |
|||
Успешно сдали: |
Не удовлетворительно: |
|||
Посещающие занятия |
19 |
16 (a) |
3 (b) |
|
Не посещающие занятия |
7 |
2 (c) |
5 (d) |
|
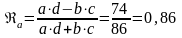 ;
;
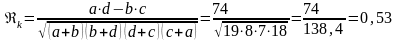
Связь
между двумя качественными признаками
считается значимой, если коэффициент
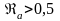 ,
а
,
а
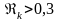 .
.
Глава 8. Выборочное наблюдение
Выборочным
называют не сплошное наблюдение, при
котором обследованию и изучению
подвергаются не все единицы исходной
совокупности, а только часть единиц,
при этом результат обследования части
совокупности распространяется на всю
исходную совокупность. Совокупность,
из
которой производится отбор единиц для
дальнейшего обследования и изучения
называется
генеральной
и все показатели, характеризующие эту
совокупность, называются генеральными.
Средняя величина признака в генеральной
совокупности обозначается через
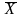 ,
а численность единиц в генеральной
совокупности обозначается через N.
,
а численность единиц в генеральной
совокупности обозначается через N.
Совокупность
отобранных единиц называется выборочной
и все показатели, характеризующие эту
совокупность, называются выборочными.
Средняя величина признака в выборочной
совокупности обозначается через
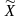 ,
а численность единиц выборочной
совокупности обозначается через n.
,
а численность единиц выборочной
совокупности обозначается через n.
Возможные пределы отклонений выборочной средней величины от генеральной средней величины называют ошибкой выборки. Чем больше ошибка выборки, тем в большей степени выборочные показатели отличаются от генеральных.
Задача
выборочного наблюдения состоит в том,
чтобы на основе данных выборочной
совокупности дать верное представление
о генеральной совокупности, т. е.
необходимо максимально приблизить
выборочные показатели к генеральным и
знать возможный предел отклонений этих
величин. При прочих равных условиях чем
больше численность единиц выборочной
совокупности, тем меньше величина ошибки
выборки. Средняя ошибка выборки
обозначатся буквой
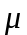 и характеризует среднюю величину
отклонений выборочных показателей от
генеральных и при этом должно соблюдаться
следующее соотношение:
и характеризует среднюю величину
отклонений выборочных показателей от
генеральных и при этом должно соблюдаться
следующее соотношение:
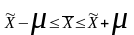 .
.
Так
как средняя ошибка выборки характеризует
среднюю величину возможных отклонений
выборочных показателей от генеральных,
то всегда найдутся единицы генеральной
совокупности, которые будут выходить
за возможные пределы, такие, как
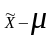 и
и
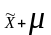 .
.
Если
мы увеличим возможные пределы отклонений
выборочных показателей от генеральных,
то с большей вероятностью сможем
утверждать, чтот показатели генеральной
совокупности отличаются от выборочных
показателей не более чем на какую-нибудь
величину, которую называют предельной
ошибкой выборки. Предельная ошибка
выборки обозначается буквой
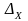 и вычисляется по формуле
и вычисляется по формуле
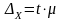 ,
где
,
где
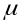 - средняя ошибка выборки; t
– коэффициент доверия, зависящий от
вероятности, с которой можно гарантировать,
что предельная ошибка выборки не превысит
t-кратную
среднюю ошибку, и всегда будет соблюдаться
следующее неравенство:
- средняя ошибка выборки; t
– коэффициент доверия, зависящий от
вероятности, с которой можно гарантировать,
что предельная ошибка выборки не превысит
t-кратную
среднюю ошибку, и всегда будет соблюдаться
следующее неравенство:
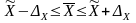 .
.
Таблица для справки:
Процент вероятности |
Коэффициент доверия (t) |
68,3% |
1,0 |
95,0% |
1,96 |
95,4% |
2,0 |
99,0% |
2,58 |
99,7% |
3,0 |
99,9% |
3,28 |
По способу отбора единиц в выборочную совокупность различают следующие виды выборочного наблюдения (выборки):
собственно-случайная
механическая
типическая
серийная
По методу отбора единиц в выборочную совокупность различают повторный и бесповторный отбор.
При повторном отборе обследованная единица после изучения вновь возвращается в генеральную совокупность и не исключена возможность дальнейшего отбора этой единицы в выборочную совокупность.
При бесповторном отборе обследованная единица не возвращается в генеральную совокупность и не участвует в дальнейшем отборе единиц в выборочную совокупность.
1) Собственно-случайная выборка заключается в том, что отбор единиц в выборочную совокупность производится без определенной системности, например, методом жеребьевки. При этом каждая единица генеральной совокупности имеет одинаковую вероятность быть отобранной в выборочную совокупность. Средняя ошибка выборки рассчитывается по формулам:
Для
повторного отбора:
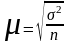 ;
для бесповторного отбора:
;
для бесповторного отбора:
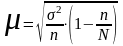 ;
где
-
дисперсия выборочной совокупности.
;
где
-
дисперсия выборочной совокупности.
2) Механическая выборка является разновидностью собственно-случайной выборки и заключается в том, что вся генеральная совокупность разбивается на определенное количество равных частей и затем из каждой части случайным образом производится отбор единиц в выборочную совокупность. Для определения средней ошибки выборки применяют те же формулы, что и при собственно-случайной выборке.
3) Типическая выборка проводится в тех случаях, когда вся генеральная совокупность разбивается на качественно-однородные группы и затем из каждой группы, случайным или механическим образом производится отбор единиц в выборочную совокупность.
Формула
для повторного отбора:
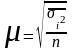 ;
для бесповторного отбора:
;
для бесповторного отбора:
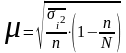 ;
где
;
где
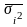 -
средняя из внутригрупповых дисперсий.
-
средняя из внутригрупповых дисперсий.
4)
Серийная выборка
состоит в том, что обследованию
подвергаются не отдельные единицы
совокупности, а целые группы или серии
единиц. При этом, в данной группе
обследованию подвергаются все единицы.
Средняя ошибка выборки определяется
по формулам: Для повторного отбора:
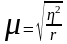 ;
для бесповторного отбора:
;
для бесповторного отбора:
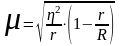 ;
где
;
где
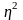 -
межгрупповая дисперсия; r
– количество групп или серий в выборочной
совокупности; R
– количество групп или серий в генеральной
совокупности.
-
межгрупповая дисперсия; r
– количество групп или серий в выборочной
совокупности; R
– количество групп или серий в генеральной
совокупности.
Для определения необходимой численности единиц в выборочной совокупности используют формулы, применяемые для расчета средней ошибки выборки.
