15. Равномерное распределение. Плотность распределения. Функция распределения. Математическое ожидание и дисперсия равномерно распределенной случайной величины.

Распределение вероятностей называется равномерным, если его функция плотности постоянна на интервале (a,b).

Дифференциальная функция распределения:

Интегральная функция распределения:

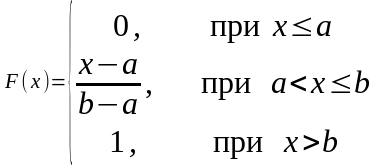
Плотность распределения имеет вид:

  

Математическое ожидание равномерно распределенной случайной величины в интервале (a;b) вычисляется по формуле:

Дисперсия равномерно распределенной случайной величины в интервале (a;b) вычисляется по формуле:

16. Биноминальное распределение. Математическое ожидание и дисперсия равномерно распределенной случайной величины.

Пусть производятся повторные независимые испытания: подбрасывание монеты, измерение температуры, рождение детей стрельба по цели и т.п., А – событие, которое может появиться в результате каж­дого испытания; для каждого единичного испытания Р(А) = р; Р( ) = q = 1 – р;

n – количество независимых повторных испытаний, К – число появления события А: Х = К – биномиальная случайная величина, она дискретна. Ее значения: К = 0; 1; 2; …

Соответствующие им вероятности находим по формуле Бернулли:

Закон распределения биномиальной случайной величины имеет вид:

P_n(0) + P_n(1) + P_n(2) + … + P_n(n) =

Основные характеристики биномиальной случайной величины:

M(X) = np; D(X) = npq;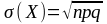

Математическое ожидание равномерно распределенной случайной величины в интервале (a;b) вычисляется по формуле:

Дисперсия равномерно распределенной случайной величины в интервале (a;b) вычисляется по формуле:

17. Показательное распределение. Плотность распределения. Функция распределения. Математическое ожидание и дисперсия показательно распределенной случайной величины.

Непрерывная случайная величина Х имеет показательное распределение с параметром l > 0, если она принимает только неотрицательные значения, а ее плотность распределения p (x )и функция распределения F (x) имеют соответственно вид:

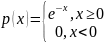
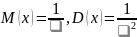
18. Нормальное распределение. Плотность распределения. Математическое ожидание и дисперсия нормально распределенной случайной величины. График нормального распределения.

Нормальное распределение (распределение Гаусса) является предельным случаем почти всех распределений вероятностей.

Нормальное распределение играет исключительно важную роль в теории вероятностей и математической статистике.

Случайная величина Х нормально распределена с параметрами a и b , b > 0, если ее плотность распределения p (x ) и функция распределения F (x) имеют соответственно вид:

;

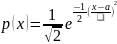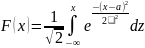
Графиком нормального распределения является кривая Гаусса:

19. Закон больших чисел.

Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке академика А.Н. Колмогорова, совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату, почти не зависящему от случая. Другими словами, при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности.

Под законом больших чисел в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.

Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли (и некоторые другие теоремы). Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли—простейшим.

Закон больших чисел впервые был сформулирован Чебышевым, а затем дополнен и обобщен его учениками – Ляпуновым и Марковым. Дальнейшее развитие этот закон получил в трудах Бернштейна, Хинчина, Гнеденко и других. Выражается этот закон несколькими теоремами, смысл которых заключается в следующем:

1. Чем больше производится испытаний, тем меньше приближенное найденное среднее значение случайной величины отличается от ее истинного значения.

2. Для характеристики большой совокупности однородных объектов не обязательно изучать всю совокупность, а можно изучить лишь часть ее (сделать выборку), причем с вероятностью близкой к 1 можно утверждать, что характеристики этой выборки сколь угодно мало отличаются от характеристики всей совокупности.

3. При достаточно большом количестве испытаний сумма независимых испытаний n, независимых случайных величин х₁ + х₂ + х₃ + … + х_n будет иметь закон распределения сколь угодно близкий к нормальному, если только max(x_i – M(x_i))  C, где С = const – смысл центральной предельной теоремы Ляпунова.