
- •51. Статистический и термодинамический методы исследования вещества.
- •52. Основные положения молскулярно-кинетичсской теории.
- •53. Максвелловский закон распределения молекул газа по их скоростям.
- •54. Больцмановский закон распосделсния молекул газа по их энергиям.
- •55. Закон равномерного распределения энергии по степеням свободы молекул газа.
- •56. Молекулярно-кинстическое толкование абсолютной температуры
- •57. Первое начало термодинамики.
- •58. Адиабатический процесс.
- •59. Политропические процессы
- •60. Второе начало термодинамики.
- •61. Изопроцессы. Запишите уравнения состояния идеального газа для этих процессов и начертите их графики в координатах р и V, р и t, t и V.
- •62. Дайте определение полной, молярной и удельной тсплоемкостей газа.
- •63Дайте определение равновесного и неравновесного состояния системы.
- •64. Дайте определение обратимого и необратимого процесса.
- •65. Дайте определение кругового процесса (цикла). Объясните принцип действия тепловых машин.
- •66. Начертите цикл Карно в координатах р и V
- •67. Дайте определение энтропии. Чему равно изменение энтропии для обратимых и необратимых процессов.
- •Энтропия и второе начало термодинамики
- •73. Приведите барометрическую формулу. Для чего она служит?
- •74. Получите формулу для средней длины свободного пробега молекул газа.
- •75. Какое явление переноса в идеальном газе описывается выражением
- •78. Получите выражения для молярных теплоемкостей всех изопроцессов в идеальном газе. 79Получите соотношение Манера
- •Соотношение Майера
- •Соотношение Майера
- •94. Начертите изотерму Ван-дер-Ваальса и сравните ее с экспериментальной изотермой реального газа.
- •95. Дайте определение критического состояния газа. Получите выражения для параметров критического состояния газа.
- •96. Получите формулу для внутренней энергия реального газа.
- •97. В чем заключается эффект Джоуля-Томсона?
- •98. Получите уравнение Клапейрона-Клаузиуса для фазового превращения реального газа.
- •99. Нарисуйте диаграмму равновесных давлений и температур для двухфазной системы "жидкость - пар".
- •100Нарисуйте обобщенную диаграмму состояний для трехфазной системы "твердое тело - жидкость - газ". Дайте определение тройной точки.
- •Фазовые превращения реального газа
- •Уравнение Клапейрона-Клаузиуса и фазовая диаграмма для превращения жг
- •Уравнение Клайперона-Клаузиуса и Рис. 6 фазовая диаграмма для превращения тж
- •Уравнение Клайперона-Клаузиуса и фазовая диаграмма для превращения тг. Тройная точка. Диаграмма состояния.
67. Дайте определение энтропии. Чему равно изменение энтропии для обратимых и необратимых процессов.
Энтропия
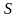 – это такая функция состояния, дифференциал
которой определяется отношением:
– это такая функция состояния, дифференциал
которой определяется отношением: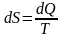 .
.
В СИ энтропия измеряется в Дж/К.
Приведём формулы для подсчёта изменения энтропии в случае изопроцессов для идеального газа:
а)
Изохорический процесс:
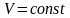
 ,
,
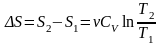 .
.
б)
Изобарический процесс:
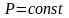
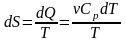 ,
,
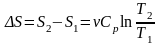 .
.
в)
Изотермический процесс:
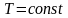
,
 .
.
г) Адиабатический процесс:
,
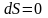 ,
,
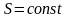 .
.
Энтропия и второе начало термодинамики
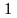 -
адиабатический процесс,
-
адиабатический процесс,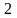 -
изохорический процесс,
-
изохорический процесс,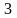 -
изобарический процесс,
-
изобарический процесс, -
изотермический процесс.
-
изотермический процесс. или термодинамической
вероятностью макросостояния.
В статистической физике существует
теорема, которая утверждает о
равновероятности всех микросостояний
данной системы. В качестве характеристики
вероятности состояния можно было бы
выбрать статистический вес
,
однако такая характеристика не обладала
бы свойствами аддитивности. Поэтому в
качестве характеристики состояния
принимается величина S,
пропорциональная логарифму статистического
веса
.
или термодинамической
вероятностью макросостояния.
В статистической физике существует
теорема, которая утверждает о
равновероятности всех микросостояний
данной системы. В качестве характеристики
вероятности состояния можно было бы
выбрать статистический вес
,
однако такая характеристика не обладала
бы свойствами аддитивности. Поэтому в
качестве характеристики состояния
принимается величина S,
пропорциональная логарифму статистического
веса
.
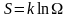 ,
(
,
(
где
 - постоянная Больцмана. Такую величину
называют энтропией.
- постоянная Больцмана. Такую величину
называют энтропией.
Определённая таким образом энтропия обладает следующими свойствами:
Энтропия изолированной системы при протекании необратимого процесса возрастает. Действительно, изолированная, т.е. предоставленная самой себе, система переходит из менее вероятных в более вероятные состояния, что сопровождается ростом величины (4).
Энтропия системы, находящейся в равновесном состоянии, максимальна.
Э![]() ти
утверждения и составляют содержание
второго
начала термодинамики:
ти
утверждения и составляют содержание
второго
начала термодинамики:
Энтропия
изолированной системы может только
возрастать, (либо по достижении
максимального значения оставаться
неизменной), т.е.
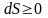 .
.
Итак, при протекании в изолированной системе необратимого процесса энтропия возрастает, т.е.
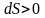 .
(5)
.
(5)
В
статистической физике доказывается,
что в ходе обратимого процесса,
сопровождающегося сообщением системе
количества теплоты
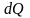 ,
энтропия системы получает приращение
,
,
энтропия системы получает приращение
,
что совпадает с принятым ранее определением энтропии .
В
определении (6) весьма существенна
обратимость процесса, в ходе которого
системе сообщается теплота
.
Если количество теплоты
сообщается системе в ходе необратимого
процесса, энтропия возрастает как
вследствие сообщения тепла, так и
вследствие необратимости процесса.
Поэтому имеет место неравенство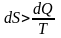 .
.
Под
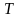 в (7) подразумевается температура
резервуара, от которого данная система
получает теплоту
.
в (7) подразумевается температура
резервуара, от которого данная система
получает теплоту
.
68. Объясните, в чем заключается статистический смысл второго начала термодинамики.
69Начертите графики изопроцессов в координатах Т иS . Получите формулы для подсчета изменения энтропии идеального газа для изопроцессов. Начертите графики эих процессов в координатах TиS
70. Начертите цикл Карно в координатах Т и S. Приведите теорему Карно.
71. Получите формулу для внутренней энергия идеального газа.
а) Внутренняя энергия идеального газа равна ,
где - количество вещества, i – число степеней свободы молекул газа.
Тогда изменение внутренней энергии газа равно - изменение внутренней энергии газа.
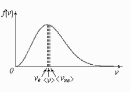
72. Приведите формулы для характерных скоростей молекул газа
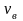 -
наиболее
вероятная скорость
молекул
-
наиболее
вероятная скорость
молекул
Это скорость молекул, при которой функция распределения имеет максимум. Возьмем производную от , и приравняв ее нулю, получим уравнение для нахождения :
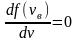 ,
,
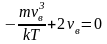 ,
,
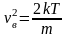 ,
,
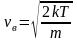 -
-
- наиболее вероятная скорость молекул
<vкв> - средняя квадратичная скорость молекул.
Для нахождения <vкв> можно воспользоваться выражением для средней кинетической энергии <> поступательного движения молекул
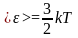 ,
,
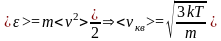 ,
,
или вычислить интеграл
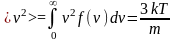
 -
средняя
квадратичная скорость молекул
-
средняя
квадратичная скорость молекул
<v> - средняя арифметическая скорость молекул.

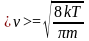 -
средняя
арифметическая скорость молекул
-
средняя
арифметическая скорость молекул
Воспользовавшись
соотношением
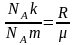 ,
формулы для характерных скоростей
молекул можно представить в виде
,
формулы для характерных скоростей
молекул можно представить в виде
 -
наиболее
вероятная скорость молекул,
-
наиболее
вероятная скорость молекул,
 -
средняя
квадратичная скорость молекул,
-
средняя
квадратичная скорость молекул,
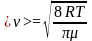 -
средняя
арифметическая скорость молекул.
-
средняя
арифметическая скорость молекул.
