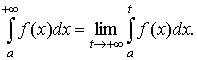- •Вопросы к экзамену по математическому анализу (2 семестр) Вопросы по теме «Неопределенный интеграл»
- •1. Интегралы вида
- •2. Интегралы вида
- •3. Интегралы вида
- •Вопросы по теме «Определенный интеграл»
- •Вопросы по теме «Функции нескольких переменных»
- •Образец экзаменационного билета
- •Часть 1 (на оценку 3). Засчитывается правильный выбор ответа из предложенных справа в таблице, но только при наличии решения.
- •Часть 2 (на оценку 4 и 5, ответ устный, не исключаются дополнительные вопросы по определениям, теоремам).
1. Интегралы вида
Тригонометрическая подстановка:
![]()
2. Интегралы вида
Тригонометрическая подстановка:
![]()
3. Интегралы вида
Тригонометрическая подстановка:
![]()
Вместо тригонометрических подстановок в случаях 1, 2, 3 можно использовать, соответственно, подстановки x = r cos t, x = r ctg t, x = r cosec t.
Интегрирование тригонометрических функций.
«Неберущиеся» интегралы.
В математическом анализе существует ряд классических выражений, интегралы от которых не выражаются через элементарные функции. То есть не существует такого выражения, которое можно записать с помощью арифметических операций и основных функций, производная которого будет равна заданной функции.
В качестве стандартных примеров можно привести следующие интегралы: интегральный синус(sin(x)/x), интеграл ex2
Вопросы по теме «Определенный интеграл»
Определение интегральной суммы для заданной функции на данном отрезке, ее геометрическая интерпретация.
Пусть на отрезке [а, b] заданна функция у = f(x). Разобьем отрезок [а, b] на n элементарных отрезков точками x0, x1,…, xn:a = x0 < x1 < x2 < … < xn = b. На каждом отрезке [xi - 1, xi] разбиения выберем некоторую точку ξ i и положим Δ xi = xi - xi - 1, где i = 1, 2,…, n. Сумму вида
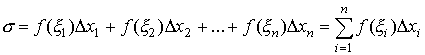
будем называть интегральной суммой для функции у = f(x) на [а, b]. Очевидно, что интегральная сумма зависит как от способа разбиения отрезка [а, b] точками x0, x1,…,xn, так и от выбора точек ξ1, ξ2, … ξn на каждом из отрезков разбиения [x i - 1, xi], i = 1, 2, …, n.
Г.с. площадь под кривой
Определение определенного интеграла, его геометрическая интерпретация.
Если существует конечный предел I интегральной суммы при λ → 0, и он не зависит от способа выбора точек ξ i, способа разбиения отрезка, то этот предел называется определенным интегралом от функции f (x)по отрезку [a, b] и обозначается следующим образом:
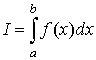 Геометрический
смысл определенного интеграла.
Если f(x)
непрерывна и положительна на [a, b],
то интеграл
Геометрический
смысл определенного интеграла.
Если f(x)
непрерывна и положительна на [a, b],
то интеграл
![]()
![]()
представляет собой площадь криволинейной трапеции, ограниченной линиями
Постройте фигуру, площадь которой численно равна
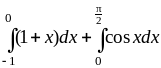 .
.Теорема существования определенного интеграла (достаточные условия интегрируемости функции), необходимое условие интегрируемости функции.
Для
существования определенного интеграла
необходимо и достаточно, чтобы ![]() .
.
Свойства определенного интеграла (с доказательством): касающиеся отрезка интегрирования, свойств или характера функции, служащие для оценки интеграла; сравнить со свойствами неопределенного интеграла. Привести примеры применения этих свойств. Поясните геометрический смысл этих свойств.
Пусть
функция
не
ограничена на отрезке ![]() .
Тогда эта функция
не
может быть интегрируемой на
,
то есть не существует предела интегральных
сумм для функции
при
условии
.
Тогда эта функция
не
может быть интегрируемой на
,
то есть не существует предела интегральных
сумм для функции
при
условии ![]() .
Иными словами, если функция интегрируема,
то она ограничена.
.
Иными словами, если функция интегрируема,
то она ограничена.
Не вычисляя, сравните интегралы:
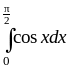 и
и
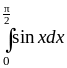 ,
,
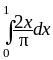 и
и
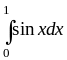 ,
,
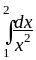 и
и
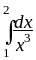 .
.Определить знаки интегралов, не вычисляя их:
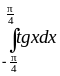 ,
,
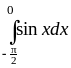 .
.
Интегрирование по частям и замена переменных в определенном интеграле, сходство и отличие от соответствующих методов в неопределенном интеграле.
Теорема Барроу (с доказательством); вывод формулы Ньютона-Лейбница. Что выражает эта формула, для чего она служит. Всегда ли может быть использована?
Если f непрерывна,
то 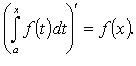 (барроу)
(барроу)
Формула Ньютона-Лейбница (формула двойной подстановки)
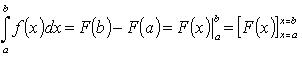
(f непрерывна; F - первообразная для f).
Несобственные интегралы: с бесконечными пределами и от неограниченной функции – их определение, сходимость, признаки сходимости, геометрическая интерпретация.
Несобственным интегралом (интегралом первого рода) от функции f(x) на полуинтервале [а, +∞) называется предел
Если предел, стоящий в правой части равенства (9.1), существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу), в противном случае — расходящимся.
Несобственный интеграл на интервале (-∞ , +∞) определяется следующим образом
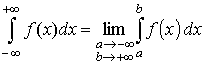 (9.3)
(9.3)
Интеграл 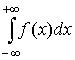 называется
сходящимся, если существует конечный
предел справа как предел функции двух
переменных. Если предела нет, то
несобственный интеграл
называется
расходящимся.
называется
сходящимся, если существует конечный
предел справа как предел функции двух
переменных. Если предела нет, то
несобственный интеграл
называется
расходящимся.
Несобственным интегралам можно придать смысл площади бесконечной фигуры.
От неограниченной
Пусть функция y = f (x) непрерывна, но не ограниченая на полуинтервале [a, b). Определение. Если существует и конечен предел
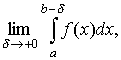 ,
,
где
δ > 0, то он называется несобственным
интегралом (несобственным интегралом
второго рода) от функции y = f (x)
на [а, b)
и обозначается 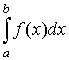 ,
т.е.
,
т.е.
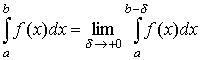 (9.5)
(9.5)
В этом случае данный несобственный интеграл (9.5) называется сходящимся, в противном случае — расходящимся. Аналогично вводится понятие несобственного интеграла от функции y = f(x) непрерывной, но неограниченной на (а, b]:
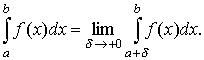 (9.6)
(9.6)
Приложения определенного интеграла к решению задач о вычислении: площади криволинейной трапеции, криволинейного сектора, объема тел вращения, длины дуги, работы силы, давления на погруженную в жидкость пластину, моментов инерции тела, статических моментов и т .п.
Известно, что f(x) – непрерывная на [a, b] функция и
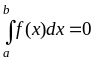 .
Следует ли отсюда, что f(x)0
на [a, b]?
Ответ обоснуйте.
.
Следует ли отсюда, что f(x)0
на [a, b]?
Ответ обоснуйте.Существуют ли площади неограниченных фигур, изображенных на рисунках ?


![]()
![]()

2


9
Доказать: а)
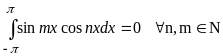 ,
б)
,
б)
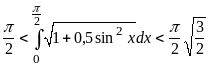
в)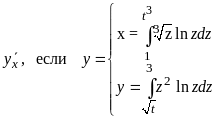 .
.
Исходя из геометрического смысла определенного интеграла, найти
а)
![]() ,
* б)
,
* б)
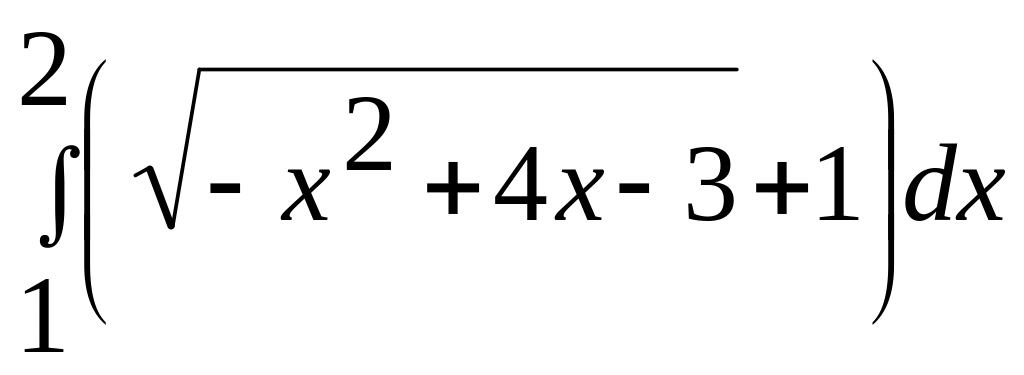 .
.