
- •1.Метрические пространства, неравенство Коши-Шварца.
- •2. Метрические пространства. Основные определения.
- •3.Векторное пространство с нормой. Евклидово пространство, понятие полноты.
- •5. Предел отображения в точке. Свойства отображений, имеющих предел в точке.
- •6.Предел и арифметические операции. Критерии Коши существования предела отображения в точке.
- •7. Предел по множеству. Предел по направлению.
- •8. Непрерывность отображений. Локальные свойства непрерывных отображений.
- •9. Равномерная непрерывность. Глобальные свойства непрерывных отображений.
- •10. Частные производные. Дифференцируемость отображений. Структура матрицы дифференциала.
- •12. Необходимые, достаточные условия дифференцируемости отображений.
- •14. Дифференциал функции нескольких переменных. Инвариантность формы первого дифференциала. Приближенные вычисления.
- •15. Геометрические приложения производной функции нескольких переменных.
- •16. Производные и дифференциалы сложных функций.
- •17. Производные высших порядков явно заданной функции
- •18.Дифференциалы высших порядков
- •19.Формула Тейлора
- •20. Формула Тейлора функции 2х переменных
- •21.Формула Тейлора с остаточным членом в формуле Пеано
- •46. Замена переменных
- •52. Знакопеременные ряды. Абсолютная и условная сходимость рядов.
- •49. Понятие о n-кратных интегралах.
- •48. Геометрические и физические приложения
- •53. Признак Абеля и Дирихле сходимости знакочередующихся рядов.
- •54. Функциональные ряды. Сходимость функциональных рядов.
- •55. Равномерная сходимость функциональных рядов. Условия равномерной сходимости.
- •56. Свойства равномерно сходящихся рядов.
- •57. Степенные ряды. Радиус сходимости. Формула Коши-Адамара.
- •58. Равномерная сходимость степенных рядов. Почленное дифференцирование и интегрирование степенных рядов.
- •59. Разложение элементарных ф-ций в ряд Тейлора (Маклорена)
- •60. Формулы Эйлера.Формула Стирлинга. Применение степенных рядов к решению задач.
53. Признак Абеля и Дирихле сходимости знакочередующихся рядов.
Т.1(признак
Абеля): 1) пусть ряд
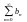 -
сходится;
2) последовательность
-
сходится;
2) последовательность
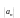 -
монотонна
и ограничена, тогда ряд
-
монотонна
и ограничена, тогда ряд
 -
сходится.
-
сходится.
Т.2(признак
Дирихле): пусть последовательность
частичных сумм ряда
ограничена,
а последовательность
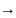 0,
при n
0,
при n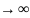 ,тогда
ряд
сходится.
,тогда
ряд
сходится.
54. Функциональные ряды. Сходимость функциональных рядов.
Рассмотрим
ряд:
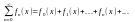 (1),где
ф-ии fk(x)
определены на множестве X
(1),где
ф-ии fk(x)
определены на множестве X ,
если зафиксировать x0
,
если зафиксировать x0 ,тогда
,тогда
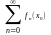 (2)-
числовой
ряд
(2)-
числовой
ряд
Опред1.
x0-точка
сходимости функционального ряда
(1),если соответственно числовой ряд
(2) сходится. Множество Е
-
область сходимости ряда (1),если (1)
сходится во
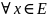 -
-
В
обл.сходимости ряд (1) сходится к некоторой
ф-ии: S(x)=
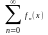 -(3),
для
,
(3)-сума ряда (1).
-(3),
для
,
(3)-сума ряда (1).
Опред2.
Последовательность Sn(x)
сходится на множестве Е равномерно
ф-ии S(x),если
выполнены условия: что для
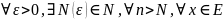 следует,что |Sn(x)-S(x)|
следует,что |Sn(x)-S(x)|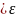 .
.
Sn(x)
S(x)
при n
,
Sn(x)=
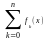 ,тогда
|S(x)-Sn(x)|=|
,тогда
|S(x)-Sn(x)|=|
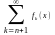 |=|rn(x)|.
|=|rn(x)|.
Если
(3) сходится к Sn(x)
равномерно на Е,то rn(x)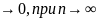 на Е.
на Е.
55. Равномерная сходимость функциональных рядов. Условия равномерной сходимости.
Критерий
Коши: для
того,чтобы : S(x)=
равномерно
сходился к S(x)
при n
на Е,необходимо и достаточно,чтобы для
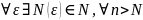 ,
,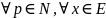
выполнялось
неравенство: |
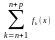 |
.
|
.
признаком равномерной сходимости ряда является признак Вейерштрасса:
если
члены ряда
(1)
удовлетворяют
неравенствам |fn(x)|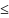 an
,
an
,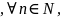
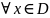 ,
и числовой ряд
,
и числовой ряд
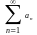 сходится,то
ряд (1) равномерно сх. в D.
сходится,то
ряд (1) равномерно сх. в D.
Теорема:
1)признак Абеля: пусть
ряд
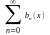 сходится
равномерно на Е, а последовательность
аn
(x)-
ограничена и монотонна на Е,тогда
сходится
равномерно на Е, а последовательность
аn
(x)-
ограничена и монотонна на Е,тогда
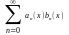 -сходится
равномерно.
-сходится
равномерно.
2)признак
Дирихле: пусть
последовательность частичных сумм
Sn(x)
ряда
ограничена
на множестве Е,последовательность аn
(x)-
ограничена
на Е монотонно и равномерно на Е,тогда ряд
сходится
равномерно на Е.
на Е,тогда ряд
сходится
равномерно на Е.
56. Свойства равномерно сходящихся рядов.
Т1.
Если ф-ция fn(x),
где х
Е непрерывна в т. х0
E
и ряд
 равномерно сходится на Е, то его сумма
S(x)
=
также
непрерывна в т. х0.
равномерно сходится на Е, то его сумма
S(x)
=
также
непрерывна в т. х0.
Т2 .(Об почленном интегрировании ряда):
Если
функциональный ряд
с
непрерывными членами сходится ф-ии
S(x)
равномерно на отрезке [a,b],
то его можно почленно интегрировать
на
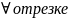 [x0,x]
[x0,x]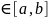 ,при этом справедливо равенство:
,при этом справедливо равенство:
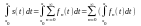 ,причем
ряд
,причем
ряд
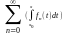 сходится
равномерно на
сходится
равномерно на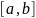 .
.
Т3. (о почленном дифференцировании ряда):
Если
ряд
(1)
с
непрерывными дифф-ми членами на
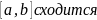 ф-ии S(x)
равномерно и ряд
ф-ии S(x)
равномерно и ряд
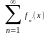 сходится
равномерно на
сходится
равномерно на
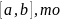 ряд (1) равномерно сходится к непрерывно
дифф-ой ф-ии S(x)
и имеет место равенство:
ряд (1) равномерно сходится к непрерывно
дифф-ой ф-ии S(x)
и имеет место равенство:
S’(x)=
(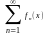 )’
,для
)’
,для
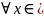 .
.
57. Степенные ряды. Радиус сходимости. Формула Коши-Адамара.
Степенным
рядом наз. функциональный ряд вида:
a0+a1x+a2x2+…
+ anxn
=
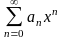 (1)
x
R,членами
которого являются степенные ф-ции.
Числа an
R
и наз. коэффициентами ряда(1). Степенным
рядом наз. также ряд: a0+a1(x-x0)+a2(x-x0)2…
+ an(x-x0)n
=
(1)
x
R,членами
которого являются степенные ф-ции.
Числа an
R
и наз. коэффициентами ряда(1). Степенным
рядом наз. также ряд: a0+a1(x-x0)+a2(x-x0)2…
+ an(x-x0)n
=
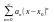 (2)
(2)
Степенной ряд (1) сходится абсолютно по крайней мере в т. х = 0, а ряд (2) в т. х = х0, т.е. в этих случаях все члены,кроме 1 равны 0. Ряд (2) сводится к ряду (1) по ф-ле у = х-х0.
Будем рассматривать степенной ряд вида (1)
Число
R>0
такое,что степенной ряд (1) сходится
абсолютно для
х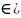 R,R)
и расходится для
х
,удовлетворяющих нер-ву |x|>R-
наз-я радиусом сходимости степенного
ряда (1) а интервал (-R,
+R)
наз. интервалом сходимости.
R,R)
и расходится для
х
,удовлетворяющих нер-ву |x|>R-
наз-я радиусом сходимости степенного
ряда (1) а интервал (-R,
+R)
наз. интервалом сходимости.
В точках x=R ,x= -R ряд может как сходиться,так и расходиться.
Если
ряд(1) сходится только в точке х=0,то
считают,что R=0,
если сходится для
х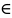 R,
то R=
R,
то R=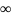 .
.
Радиус сходимости можно опред-ть,используя признак Даламбера или Коши:
1)
R=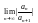
2)
R=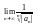 -
формула Коши-Адамара, если известно
поведение ряда в граничных точках: x1=
-R
,x2=
R,то
множество х
[-R,R]
называют областью сходимости степенного
ряда.
-
формула Коши-Адамара, если известно
поведение ряда в граничных точках: x1=
-R
,x2=
R,то
множество х
[-R,R]
называют областью сходимости степенного
ряда.
