10. Частные производные. Дифференцируемость отображений. Структура матрицы дифференциала.

В математическом анализе, частная производная — одно из обобщений понятия производной на случай функцииf нескольких переменных.

Следует обратить внимание, что обозначение следует понимать как цельный символ, в отличие от обычной производной функции одной переменной которую можно представить, как отношение дифференциалов функции и аргумента. Однако, и частную производную можно представить как отношение дифференциалов, но в этом случае необходимо обязательно указывать, по какой переменной осуществляется приращение функции: где — частный дифференциал функции f по переменной x. Часто непонимание факта цельности символа является причиной ошибок и недоразумений, как, например, сокращение в выражении .

Геометрически, частная производная является производной по направлению одной из координатных осей. Частная производная функции f в точке по координате равна производной по направлению , где единица стоит на -ом месте..

11. Частные производные. Случай функции двух переменных.

Пусть задана система функций , имеющих в некоторой точке x все частные производные первого порядка. Матрица J, составленная из частных производных этих функций в точке x, называется матрицей Якоби данной системы функций.

Если m = n, то определитель | J | матрицы Якоби называется определителем Якоби, или якобиа́ном, системы функций

Частные производные можно обозначать так же как J(x) Случай функции 2-х переменных

αf( x )=A(x)dx;A(x); α(x)=(x1…..xn)

Пусть функция z=f(x,y) дифференцируема в точке f0=(x0,y0),тогда главная относительно приращения аргументов часть его полного приращения ,наз. полным дифф-ом ее функции и обозначается :αf(Po)=(δf(Po)/dx)*x+(δf(Po)/dy)*y

Общая формула f’(x)=A(x)h+0(ρ),обозначает ,что : f’(x,y)=(df/dx , df/dy)*(h1, h2)+0(x)+0(y) x, y Заменим приращение x, y на dx и dy,тогда

df =(df/dx)*dx+(df/dy)*dy (1)

Выражения :(df/dx)*dx=dxf

(df/dy)*dy=dyf

Соответственно частные дифф-лы функции f по переменной х и у

Из (1)-формула для приближенного вычисления значения функции:f(P)=f(Po)+df(Po),для любой точки Р о нахождении в какой-то маленькой окрестности Ро.

12. Необходимые, достаточные условия дифференцируемости отображений.

Для того, чтобы функция f(x) была дифференцируема в точке x0 необходимо и достаточно, чтобы у нее существовала производная в этой точке.

При этом Δy = f(x0+Δx)-f(x0) = f '(x0)Δx+α(Δx)Δx,

где α(Δx) - бесконечно малая функция, при Δx→0.

13. Производная по направлению. Градиент.+

Определение. Вектор с координатами , , называется градиентом функции u = f (x, y, z) в точке M(x, y, z) и обозначается gradu = + + .

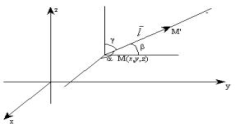
Под производной функции u = f (x, y, z) в данном направлении i понимается выражение = cosa + cosb + cosg, где cosa, cosb, cosg – направляющие косинусы вектора i (рис. 43).

Производная представляет собой скорость изменения функции в данном направлении.

Теорема. Производная функции по направлению равна проекции градиента этой функции на данное направление (в соответствующей точке).

Как известно, проекция вектора на другой вектор имеет максимальное значение, если оба вектора совпадают по направлению.

Градиент функции в данной точке указывает напрвление наиболее быстрого возрастания функции.

Величина градиента, т.е. | grad u | = обозначается tg j и определяет крутизну наибольшего ската или подъема поверхности u = f (x, y).

В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.

Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.

Рассмотрим функцию от n аргументов в окрестности точки . Для любого единичного вектора определим производную функции f в точке по направлению следующим образом:

Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора .

Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.