19.Формула Тейлора

Тейлора формула, формула

изображающая функцию f (x), имеющую n-ю производную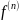 (a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена 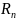(x), являющегося в окрестности точки a бесконечно малой более высокого порядка, чем 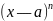[то есть (x) = 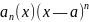, где (x) ® 0 при х ® а]. Если в интервале между а и х существует (n + 1)-я производная, то Rn (x)можно представить в видах:

где x и 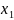— какие-то точки указанного интервала (остаточный член Т. ф. в формах Лагранжа и соответственно Коши). График многочлена, входящего в Т. ф.. имеет в точке а соприкосновение не ниже n-го порядка с графиком функции f (x). Т. ф. применяют для исследования функций и для приближённых вычислений.

20. Формула Тейлора функции 2х переменных

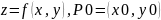
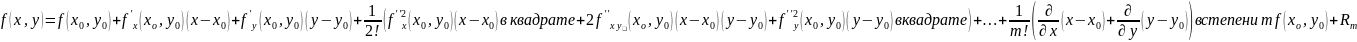
Где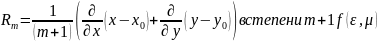

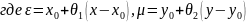
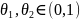
21.Формула Тейлора с остаточным членом в формуле Пеано

Теорема:

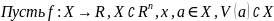
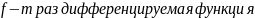
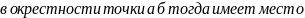
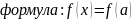
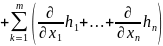
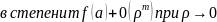
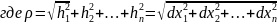
22.Пусть функция нескольких переменных u = f(x1, x2, … , xn) = f(x) определена в некоторой окрестности точки x0 = (a1, a2, … , an) .

Точка x0 называется точкой локального максимума (локального минимума) функции u = f(x) , если существует такая окрестность Oδ(x0) точки x0 , что для всех точек x ОOδ(x0) выполняется неравенство f(x) ≤ f(x0) (f(x) ≥ f(x0)) .

Значение функции u = f(x0) в этой точке называется локальным максимумом (или локальным минимумом) функции и обозначается umax (или umin ).

Если при x ≠ x0 имеет место неравенство f(x) ≠ f(x0) , то точка x0 называется точкой строгого локального максимума (минимума).

Точки максимума и минимума функции называются точками экстремума, а максимумы и минимумы — экстремумами функции.

Необходимое условие экстремума

Теорема (Необходимое условие экстремума) Если функция нескольких переменных u = f(x1, x2, … , xn) имеет экстремум в некоторой точке, то в этой точке каждая ее частная производная равна нулю или не существует.

Внутренние точки из области определения функции, в которых выполняются необходимые условия экстремума, называются критическими. Если в критической точке функция дифференцируема, то такая точка называется стационарной.

В стационарной точке (x0, y0) функции f(x, y) существуют частные производные f'x , f'y и f'x(x0, y0) = 0 , f'y(x0, y0) = 0

Достаточные условия экстремума

Пусть функция u = f(x1, x2, … , xn) имеет непрерывные частные производные до 2–го порядка включительно в некоторой окрестности ее стационарной точки M0(x10, x20, … , xn0) .

Пусть M(x10 + dx1, x20 + dx2, … , xn0 + dxn) — некоторая точка из этой окрестности. Тогда

Δu = f(x10 + dx1,x20 + dx2, … ,xn0 + dxn) − f(x10,x20, … ,xn0) — приращение функции, которое она получает при смещении из точки M0 в точку M .

По формуле Тейлора имеем Δz = dz(M0) + 1/2! d2z(M0) + o(ρ2)

где ρ — расстояние между точками M0 и M .

Так как M0 — стационарная точка функции u = f(x1, … ,xn) , то dz(M0) = 0 .

Допустим, что d2z(M0) ≠ 0 для всех точек M из некоторой окрестности Oδ(M0), достаточно малой, чтобы в ней выполнялось неравенство |d2z(M0)| > |o(ρ2)| . Тогда знаки Δz и d2z(M0) одинаковы .

Если d2z(M0)>0 для всех точек M из окрестности Oδ(M0) то и Δz> 0.

В этом случае функция u = f(x1, … , xn) имеет минимум в точке M0 .

Если d2z(M0)<0 для всех точек M из окрестности Oδ(M0), то и Δz< 0.

В этом случае функция u = f(x1, … ,xn) имеет максимум в точке M0 .

Таким образом, достаточным условием экстремума функции нескольких переменных в ее стационарной точке является знакоопределенность (положительная или отрицательная определенность) дифференциала 2–го порядка в этой точке.

23.Пусть функция u=f(x,y) –критическая точка функции U. Значит в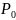 имеют место равенства: 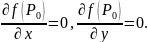Обозначим через

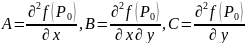
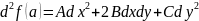
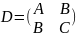
Следовательно: 1) при

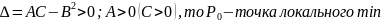
2)при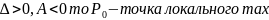

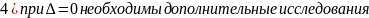
24.Неявные функции

Рассмотрим систему 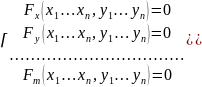(1)Выясним при каких условиях можно найти из этой системы функции: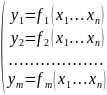 (2)Такие, что подставляя ихв исходную систему (1) будем получать верные тождества.

Введём векторы: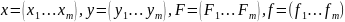 Тогда (1) и (2) примут вид: .

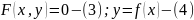Обозначим через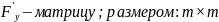

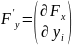Теорема: Пусть система (3) обладает свойствами:

1. Все функции

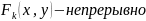
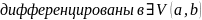
2. Сама функция

3. 

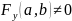
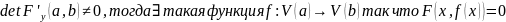
Если V(a)достаточно мала, то 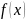определиться однозначно.

Функция непрерывно дифференцируема в достаточно малом V(a) при этом выполнено равенство :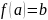

25. Производные неявных функций. Зависимость функций.

В курсе математического анализа доказано, что неявная функция существует (однако не всегда), у неё есть график (точно так же, как и у «нормальной» функции). У неявной функции точно так же существует первая производная, вторая производная и т.д.

Найти производную от функции, заданной неявно

Навешиваем штрихи на обе части:

Используем правила линейности:

Находим производные:

Раскрываем все скобки:

Переносим все слагаемые с 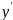в левую часть, остальные – в правую часть:

В левой части выносим за скобку:

Окончательный ответ:

Понятие зависимости функций. Пусть m функций от одних и тех же n переменных

u₁ = φ₁(x₁, x₂, …, x_n); u₂ = φ₂(x₁, x₂, …, x_n)

…………………………

u_m = φ_m(x₁, x₂, …, x_n)

определены и дифференцируемы в некоторой открытой n-мерной об­ласти D (В частности, в качестве области D можно взять некоторую окрест­ность фиксированной точки M₀ n-мерного пространства.

Будем говорить, что одна из этих функций, например u_k, зави­сит в области D от остальных функций, если сразу для всех точек (x₁, x₂, …, x_n) области D

u_k = Ф(u₁, …, u_k-1, u_k+1 …, u_m)

где Ф — некоторая функция, определенная и дифференцируемая в соответствующей области изменения своих аргументов. Функции u₁, u₂, …, u_m будем называть зависимыми в области D, если одна из этих функций (все равно какая) зависит в области D от остальных.

Если же не существует дифференцируемой функции Ф такой, что сразу для всех точек области D справедливо тождество ви­да (29), то мы будем называть функции u₁, u₂, …, u_m независи­мыми в области D.

26. Неявные функции, определяемые системой уравнений. Замена переменных.

Рассмотрим n штук функций: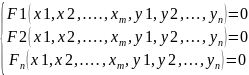 (37)

И пусть по смыслу задачи 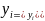), i=1,2,…,n. (38)

Как и прежде нас будет интересовать вопрос о существовании неявной функций (38),заданных системой(37),о единственности и прочих свойствах.

Чтобы сформулировать соответствующую теорему нам понадобится понятие якобина.

Опред.Пусть заданы n функций 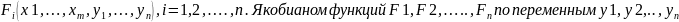называется определитель,составленный из частных производных

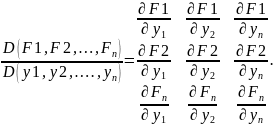
Теорема.Пусть функция 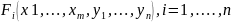удовлетворяют следующим условиям

1) (

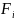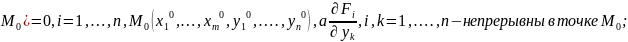
2)Дифференцируемы в окрестности точки

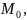
3)Определитель Якоби

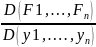
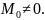
Тогда система уравнений (37) однозначно определяет в некоторой окрестности точки

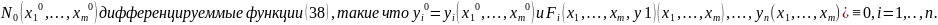
Замена переменной

Одним из главных способов преобразования неопределенных интегралов к табличным является метод замены переменной. Он имеет два варианта. Первый вариант используется после подведения под знак дифференциала, когда имеется равенство

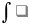U(x) · V'(x) dx = ∫ U(x) dV(x) .

Если функция U(x) выражается через функцию V(x) по некоторой формуле U(x) = w(V(x)), то

U(x) dV(x) = ∫ w(V(x)) dV(x) = ∫ w(t) dt где t = V(x). Таким образом отыскание исходного интеграла сводится к отысканию интеграла

w(t) dt

В нем функция t = V(x) выступает как независимая переменная, т.е. произошла замена переменной. Новая переменная t вводится как функция исходной переменной x. Не требуется, чтобы соответствие между x и t было взаимно однозначным.

27. Условный экстремум. Метод множителей Лагранжа.

Условный экстремум. Пусть функция

u = f(x1, x2, … , xn) (1)

определена в некоторой области D М Rn и ее аргументы не являются независимыми переменными, а связаны k (k<n) соотношениями:

Fi(x1, x2, … , xn) = 0 (i = 1,2, … ,k). (2)

Условия (2) называются уравнениями связи.

Пусть координаты точки M0(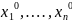 ) О D удовлетворяют уравнениям связи (2).

Точка M0( ) называется точкой условного максимума (минимума) функции (1) при условиях связи (2), если существует такая окрестность Oδ(M0) точки M0 , что для любой точки M(x1, … ,xn) О Oδ(M0) , координаты которой удовлетворяют уравнениям связи (2), выполняется неравенство f(M) ≤ f(M0) (f(M) ≥ f(M0)) .

Лагранжа метод множителей, метод решения задач на условный экстремум; Лагранжа метод множителей заключается в сведении этих задач к задачам на безусловный экстремум вспомогательной функции — т. н. функции Лагранжа.

Для задачи об экстремуме функции f (х1, x2,..., xn) при условиях (уравнениях связи) ji(x1, x2, ..., xn) = 0, i = 1, 2,..., m, функция Лагранжа имеет вид

Множители y1, y2, ..., ym наз. множителями Лагранжа.

Если величины x1, x2, ..., xn, y1, y2, ..., ym суть решения уравнений, определяющих стационарные точки функции Лагранжа, а именно, для дифференцируемых функций являются решениями системы уравнений

то при достаточно общих предположениях x1, x2, ..., xn доставляют экстремум функции f.

28. Условный экстремум. Случай функции двух переменных. Абсолютный экстремум.

Теорема (необходимое условие экстремума функции двух переменных). Если функция z=f(x,y) достигает экстремума при x=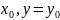 , то каждая частная производная первого порядка от z или обращается в нуль при этих значениях аргументов, или не существует.

Пусть задана функция z=f(x,y) в некоторой области D. Точка M(x,y) называется внутренней для области D, если M принадлежит области D вместе с некоторой своей окрестностью. Точка N называется граничной для области D, если для любой ее окрестности имеются точки, как принадлежащие области D, так и не принадлежащие ей. Множество всех граничных точек называется границей Г. Определение 3. Наименьшее (наибольшее) значение функции в данной области называется абсолютным экстремумом функции в этой области.

29. Несобственные интегралы с бесконечными пределами. Интегралы от неотрицательных функций. Критерий Коши. Признаки сравнения.

Несобственный интеграл с бесконечным пределом

Пусть функция f(x) непрерывна при a ≤ x < +∞. Тогда по определению полагают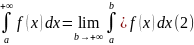

Если предел (2) существует, то несобственный интеграл с бесконечным пределом интегрирования, стоящий в левой части равенства (2), назвается сходящимся и его значение определяется формулой (2); в противном случае равенство (2) теряет смысл, несобственный интеграл, стоящий слева, называется расходящимся и ему не приписывается никакого числового значения.

Интегралы от неотрицательных функций

( Критерий Коши ) Для того, чтобы последовательность { xn } сходилась, необходимо и достаточно чтобы она была фундаментальной.

Признак сравнения — утверждение об одновременности расходимости или сходимости двух рядов, основанный на сравнении членов этих рядов.

30. Признаки абсолютной и условной сходимости. Интеграл в смысле главного значения.

Ряд 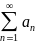называется абсолютно сходящимся, если ряд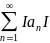 также сходится.

Если ряд сходится абсолютно, то он является сходящимся (в обычном смысле). Обратное утверждение неверно.

Ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

31тоже самые вопросы что 29

39. Двойным интегралом называют кратный интеграл с  .

. Здесь   — элемент площади в рассматриваемых координатах.

В прямоугольных координатах:  , где   — элемент площади в прямоугольных координатах.

Двойные интегралы вычисляются, как правило, с помощью повторных интегралов. Однако переход от двойных к повторным интегралам возможен не для произвольной области интегрирования R, а для областей определенного типа. Введем понятия областей интегрирования типа I и II.  Определение 1. Говорят, что область R на плоскости относится к типу I или является элементарной относительно оси Oy, если она лежит между графиками двух непрерывных функций, зависящих от x(рисунок 1), и описывается множеством:

Определение 2. Говорят, что область R на плоскости относится к типу II или является элементарной относительно оси Ox, если она лежит между графиками двух непрерывных функций, зависящих от y(рисунок 2), и описывается множеством:

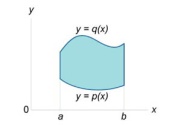
Рис.1		Рис.2

Связь между двойными и повторными интегралами

Пусть f (x,y) является непрерывной функцией в области R типа I:

Тогда двойной интеграл от функции f (x,y) в данной области выражается через повторный интеграл в виде

Для области интегрирования типа II существует аналогичная формула. Если f (x,y) является непрерывной функцией в области R типа II:

то справедливо соотношение

Приведенные формулы (в англоязычной литературе они известны как теорема Фубини) позволяют вычислять двойные интегралы через повторные. В повторных интегралах сначала находится внутренний интеграл, а затем - внешний. 

Пусть область интегрирования R представляет собой прямоугольник  . Тогда двойной интеграл в такой области выражается через повторный интеграл в следующем виде:

В данном случае область интегрирования R относится одновременно к типу I и II, так что у нас есть возможность выбирать, по какой переменной (x или y) начинать интегрировать функцию f (x,y). Обычно удобнее начинать с более простого интеграла.  В частном случае, когда подынтегральная функция  f (x,y) "расщепляется" на произведение f (x)g(y), двойной интеграл равен произведению двух определенных интегралов:

40. Двойным интегралом называют кратный интеграл с  .

. Здесь   — элемент площади в рассматриваемых координатах.

В прямоугольных координатах:  , где   — элемент площади в прямоугольных координатах.

Пусть область интегрирования R типа I (элементарная относительно оси Oy) ограничена графиками функций  . При этом выполняются неравенства   и   для всех  . Тогда двойной интеграл по области R выражается через повторный по формуле

Аналогичное соотношение существует и для области типа II. Пусть область интегрирования R типа II (элементарная относительно оси Ox) ограничена графиками функций   при условии, что   и   для всех  . Тогда двойной интеграл, заданный в области R, выражается через повторный интеграл по формуле

При решении задач иногда полезно разбить исходную область интегрирования R на две или более областей и вычислять двойной интеграл в каждой области отдельно. 

41. Якобиа́н (определитель Яко́би, функциональный определитель) — определитель матрицы Якоби:

для векторной функции   имеющей в некоторой точке   все частные производныепервого порядка (определитель Якоби или якобиан системы функций  ).

Также якобианом иногда (по-русски такое употребление термина не вполне принято) называют саму матрицу Якоби, а не её определитель.^{[источник не указан 898 дней]} По-английски и в некоторых других языках термин якобиан считается равно приложимым к матрице Якоби и её определителю

Часто используются следующие обозначения якобиана:

 или 

Определитель Якоби обычно определён для случая m = n, то есть для квадратных матриц Якоби; для m ≠ n его можно считать нулём (в простейшей интерпретации матрица Якоби дописывается при этом нулями до квадратной).

Для вычисления двойного интеграла   иногда удобнее перейти в другую систему координат.  Это может быть обусловлено формой области интегрирования или сложностью подынтегральной функции.  В новой системе координат вычисление двойного интеграла значительно упрощается.  Замена переменных в двойном интеграле описывается формулой

где выражение  представляет собой так называемый якобиан преобразования  , а S − образ области интегрирования R, который можно найти с помощью подстановки   в определение области R. Отметим, что в приведенной выше формуле  означает абсолютное значение соответствующего определителя.  Предполагая, что преобразование координат   является взаимно-однозначным, обратное соотношение описывается якобианом

при условии, что знаменатель нигде не равен 0

42. Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается  ) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается  , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.

 Обобщенными полярными координатами называется пара действительных чисел

Обобщение

Используя декартовы координаты, площадь бесконечно малого элемента может быть вычислена как  . При переходе к другой системе координат в многократных интегралах, необходимо использовать определитель Якоби:

Для полярной системы координат, определитель матрицы Якоби равен  :

Следовательно, площадь элемента в полярных координатах можно записать так:

Теперь, функция, записанная в полярных координатах, может быть интегрирована следующим образом:

Здесь область  , как и в предыдущем разделе, такая, которую образуют полярная кривая   и лучи   и  .

Формула для вычисления площади, описанная в предыдущем разделе, получена в случае  . Интересным результатом применения формулы для многократных интегралов является Интеграл Эйлера — Пуассона: