3.Векторное пространство с нормой. Евклидово пространство, понятие полноты.
Рассмотрим
пространство
и точки
.
Условимся считать, что
.
.
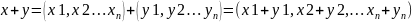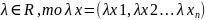Для векторов
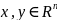имеют место свойства:
1)
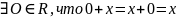
2)
3)
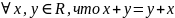4)
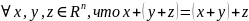
5)
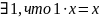
6)
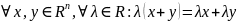
7)
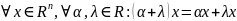
8)
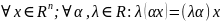
Пространство с введёнными операциями 1 и 2 и свойствами 1-8 называют векторным пространством.
ОПР.
Понятие отображения
,
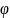отобр. множ.
,
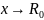где
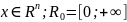называется нормой в пространстве x,
если выполнены условия:
1)
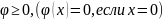
2)
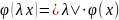
3)
Множество
х с введённой нормой называется
нормированным векторным пространством.
Норму
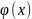будем обозначать ||x||.
В зависимости от вида пространства
норму можно задавать по разному:
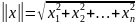- сферическая норма. Или
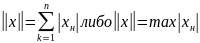
Евклидово пространство
Пусть
-векторное
пространство, функция
отобр.
,
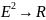где Е является подмножеством R
и обозн.
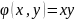наз. Скалярным произведением x,y
если выполняются свойства.
1)
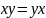
2)
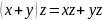
3)
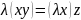
4)
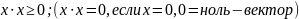
Если
,
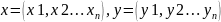то скалярное произведение xy
записывается
.
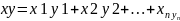Пространство
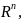для
которого задано скалярное произведение
в таком виде называется евклидовым
векторным пространством.
При
этом вводят символы:
-
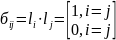
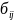символ Кронекера. Отсюда следует, что
.
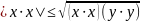Число
будем наз. длиной вектора х. Из этого
видно, что
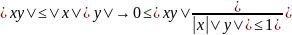
4.Понятие отображений. Понятие функций многих переменных.
Пусть
,
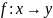(где x-некоторая
посл. из
,
а у-некоторая посл.из
)
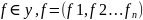
1)
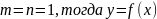
2)
-
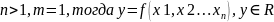функция многих переменных
3)
4)
-это
не функция а отображение.
Говорят,
что
,
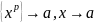при
,
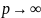если
,
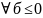можно указать такой томер N,
что для
,
точка
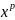будет
соед в окрестности
.
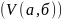Отображение
f
ограничено, если сущ. шар (B(b,R))
что
,
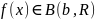а сам шар содержится в
если функция f
ограничена на х.
Понятие
функции многих переменных.
Пусть
,
тогда f: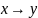
-это
функция 2-х переменных. U=f(x,y);
,
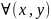множество x
и y,
при которых выражение имеет смысл
называется облостью функции . пример:
для двух переменных
Для
трёх переменных
5. Предел отображения в точке. Свойства отображений, имеющих предел в точке.
Точка
b
называется пределом отображения f
при
,
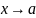если для
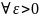найдётся такое число б>0 такое что для
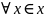таким, что
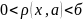будет выполнено условие что
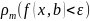при
этом записывают
.
ОПР.
точка b
наз пределом отобр f
при
,
если для
окрестность в точке b
сущ проколотая б-окрестность такая,
ччто если
.
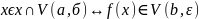ОПР.
вектор b
наз пределом отобр f
при
если для
сущ число
,
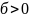что для всех
.
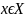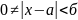выполняется неравенство
.
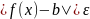ОПР.
точка b
наз пределом отображения f
при
,
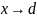если для
,
при
.
Доказательство равносильно в одномерном
случае.
Теорема 1: 1) если отображение f имеет lim в точке а, то сущ окрестность в точке а в которой f ограничено. 2)если отображение f имеет lim в точке а, то этот lim единственный.
Теорема
2: чтобы
было lim
и отобр f=(f1,fn)
при
необх и достаточно, чтобы числа
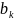были lim
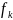при
.
,
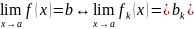для
).
6.Предел и арифметические операции. Критерии Коши существования предела отображения в точке.
Теорема
о пределе и арифметических операциях:
пусть lim
при
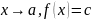и сущ lim
при
;
g(x)=c,
тогда сущ lim
f(x)+g(x)=b+c,
,
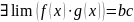где b+c,bc,f+g,
fg
–суммы и скалярные произведения соотв
векторов.
Доказательство:
пусть u-f(x),
v=g(x),
бu-n-мерный,
вектора, u=(u1,u2,…un),
v=(v1,v2…vn),
тогда |(u+v)-(b+c)|≤max|(uк•vk)-(bk+ck),
так как
,
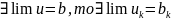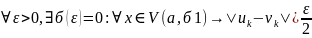так как
для
,
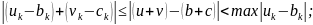
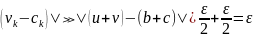где б- min
из {б1,б2}
Критерии
коши:
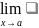отображения
,
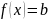тогда и только тогда, когда
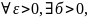такое что если x
и y
2 вектора
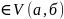то
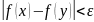
Доказательство:
докажем, что если сущ lim,
то выполняется условие из теоремы.
Пусть сущ
,
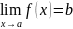для
,
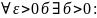
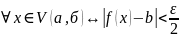тогда
оценим
,
тогда
всё выполняется.