6.3. Телеграфное уравнение,

Телеграфное уравнение в математике, дифференциальное уравнение с частными производными, описывающее при определённых упрощающих предположениях процесс распространения тока по проводу. Сила тока i и напряжение u. удовлетворяют системе Т. у. ( я хз че это за)

где x — координата, отсчитываемая вдоль провода, t — время, С, G, L и R — коэффициенты ёмкости, утечки, индуктивности, сопротивления провода, рассчитанные на единицу длины. При LC  0 соответствующая замена переменных приводит к уравнению

которое также называется Т. у. Краевые задачи для Т. у. решаются методами, разработанными для уравнения колебаний струны (см. Волновое уравнение), в которое при k = 0 переходит Т. у. При k  0 в описываемом Т. у. процессе имеет место явление дисперсии (см., например, Дисперсия звука). При решении Т. у. широко применяются операционное исчисление и специальные функции. Т. у. изучалось У. Томсоном (при L = 0, 1855), Г. Кирхгофом (в общем случае, 1857), О. Хевисайдом (1876), А. Пуанкаре (1897) и др. Наименование «Т. у.» (l'equation des telegraphistes) предложил А. Пуанкаре.

6.4. Уравнение Лапласа,

Лапласа уравнение:

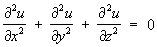
– простейшее уравнение эллиптического типа и соответствующее неоднородное уравнение – Пуассона уравнение. Уравнения и системы эллиптического типа появляются обычно при анализе стационарных состояний.

6.5. Уравнение теплопроводности

Теплопроводности уравнение:

– простейший пример уравнения параболического типа. Уравнения и системы параболического типа появляются обычно при анализе процессов выравнивания.

Первым примером уравнений смешанного типа явилось так называемое уравнение Трикоми:

Для этого уравнения полуплоскость служит зоной эллиптичности, полуплоскость у < 0 – зоной гиперболичности, а прямая у = 0 – зоной параболичности.

Ряд задач математической физики приводит к интегральным уравнениям различных типов. Так, например, интегральные уравнения Вольтерра возникают в тех задачах физики, в которых существует предпочтительное направление изменения независимого переменного (например, времени, энергии и т.д.). В задаче о крутильных колебаниях возникает некоторое интегро-дифференциальное уравнение.

Постановка задач и методы решения уравнений математической физики. На первом этапе развития теории У. м. ф. много усилий было затрачено на отыскание их общего решения. Уже Ж. Д'Аламбер (1747) получил общее решение волнового уравнения. Основываясь на подстановках, применявшихся Л. Эйлером (1770), П. Лаплас предложил (1773) «каскадный метод», дающий общее решение некоторых др. линейных однородных гиперболических уравнений 2-го порядка с двумя аргументами. Однако такое общее решение удалось найти в весьма редких случаях; в отличие от обыкновенных дифференциальных уравнений, для уравнений с частными производными не выделено ни одного сколько-нибудь значительного класса уравнений, для которых общее решение может быть получено в виде достаточно простой формулы. Кроме того, оказалось что при анализе физических процессов У. м. ф. обычно появляются вместе с дополнительными условиями, характер которых коренным образом влияет на направление исследования решения (см. Краевые задачи, Коши задача).

7.1. Устойчивость по Ляпунову, асимптотическая устойчивость.