2.2.4. Свойства решений линейного однородного дифференциального уравнения.

Теорема о линейности пространства частных решений ЛОДУ. Множество частных решений линейного однородного дифференциального уравнения образует линейное пространство. 

Пусть y₁(x), y₂(x), …, y_n(x) - частные решения линейного однородного дифференциального уравнения. Если определитель Вронского этой системы функций равен нулю в некоторой точке  , то система функций y₁(x), y₂(x), …, y_n(x) линейно зависима, и её определитель Вронского тождественно равен нулю на (a, b). 

Если определитель Вронского W(x) системы y₁(x),y₂(x), …, y_n(x) частных решений линейного однородного дифференциального уравнения отличен от нуля в некоторой точке  , то W(x) отличен от нуля в любой точке этого интервала. 

2.2.5. Фундаментальная система решений линейного однородного дифференциального уравнения.

Фундаментальной системой решений линейного однородного дифференциального уравнения n-го порядка называется любая линейно независимая система y₁(x), y₂(x), …, y_n(x) его n частных решений.  Теорема о структуре общего решения линейного однородного дифференциального уравнения. Общее решение y(x) линейного однородного дифференциального уравнения есть линейная комбинация функций из фундаментальной системы решений этого уравнения:  y(x) = C₁ y₁(x) + C₂ y₂(x) + …+ C_n y_n(x).  Из этой теоремы следует, что размерность линейного пространства частных решений однородного уравнения с непрерывными коэффициентами не превышает n. Осталось доказать, что эта размерность не меньше n.  Теорема о существовании фундаментальной системы решений линейного однородного дифференциального равнения. Любое линейное однородное дифференциальное уравнение n -го порядка с непрерывными коэффициентами имеет фундаментальную систему решений, т.е. систему из n линейно независимых решений.  .......

Итак, мы доказали, что размерность линейного пространства частных решений однородного уравнения с непрерывными коэффициентами равна n, и базисом в этом пространстве служит любая фундаментальная система решений. Общее решение такого уравнения равно линейной комбинации функций из фундаментальной системы решений. Остаётся вопрос - как находить фундаментальную систему решений; оказывается, что в общем случае это возможно только в случае уравнения с постоянными коэффициентами

2.2.6. Теорема о структуре общего решения линейного однородного дифференциального уравнения.

Теорема о структуре общего решения линейного однородного дифференциального уравнения. Общее решение y(x) линейного однородного дифференциального уравнения есть линейная комбинация функций из фундаментальной системы решений этого уравнения: 

y(x) = C₁ y₁(x) + C₂ y₂(x) + …+ C_n y_n(x). 

Док-во. Пусть y₁(x), y₂(x), …, y_n(x) - фундаментальная система решений линейного однородного дифференциального уравнения. Требуется доказать, что любое частное решение y_чо(x) этого уравнения содержится в формуле y(x) = C₁ y₁(x) + C₂ y₂(x) + …+ C_n y_n(x) при некотором наборе постоянных C₁, C₂, …, C_n. Возьмём любую точку  , вычислим в этой точке числа   и найдём постоянные C₁, C₂, …, C_n как решение линейной неоднородной системы алгебраических уравнений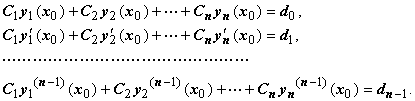   Такое решение существует и единственно, так как определитель этой системы равен  . Рассмотрим линейную комбинацию y(x) = C₁y₁(x) + C₂ y₂(x) + …+ C_n y_n(x) функций из фундаментальной системы решений с этими значениями постоянных C₁, C₂, …, C_n и сравним её с функцией y_чо(x). Функции y(x) и y_чо(x) удовлетворяют одному уравнению и одинаковым начальным условиям в точке x₀, следовательно, по единственности решения задачи Коши, они совпадают: y_чо(x) = C₁ y₁(x) +C₂ y₂(x) + … + C_n y_n(x). Теорема доказана.  Из этой теоремы следует, что размерность линейного пространства частных решений однородного уравнения с непрерывными коэффициентами не превышает n. Осталось доказать, что эта размерность не меньше n.