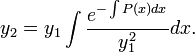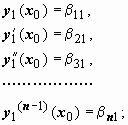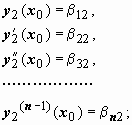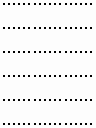2.2.7. Теорема о существовании фундаментальной системы решений линейного однородного дифференциального уравнения.

Теорема о существовании фундаментальной системы решений линейного однородного дифференциального равнения. Любое линейное однородное дифференциальное уравнение n -го порядка с непрерывными коэффициентами имеет фундаментальную систему решений, т.е. систему из n линейно независимых решений.  Док-во. Возьмём любой числовой определитель n -го порядка, не равный нулю

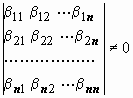
Возьмём любую точку   и сформулируем для уравнения

n задач Коши, причём начальные условия в точке x₀ для i-ой задачи возьмём из i-го столбца этого определителя:

Ln(y1) = 0;

Ln(y2) = 0;

Ln(yn) = 0;

Пусть y₁(x), y₂(x), …, y_n(x) - решения этих задач. Эта система линейно независима на (a, b), так как её определитель Вронского в точке x₀ равен взятому числовому определителю и отличен от нуля, следовательно, это фундаментальная система решений. Теорема доказана.

Итак, мы доказали, что размерность линейного пространства частных решений однородного уравнения с непрерывными коэффициентами равна n, и базисом в этом пространстве служит любая фундаментальная система решений. Общее решение такого уравнения равно линейной комбинации функций из фундаментальной системы решений. Остаётся вопрос - как находить фундаментальную систему решений; оказывается, что в общем случае это возможно только в случае уравнения с постоянными коэффициентами

2.2.8. Восстановление линейного однородного уравнения по фундаментальной системе решений.

Пусть дана система функций y₁(x), y₂(x), …, y_n(x) с отличным от нуля на отрезке (a, b) вронскианом W(x). Требуется составить линейное однородное уравнение, у которого фундаментальная система решений состоит из функций y₁(x), y₂(x), …, y_n(x).  Так как общее решение этого уравнения должно быть равно y(x) = C₁ y₁(x) + C₂ y₂(x) + …+ C_n y_n(x), система функций y(x), y₁(x), y₂(x), …, y_n(x)линейно зависима, поэтому её определитель Вронского(имеющий порядок n+1)должен быть=0 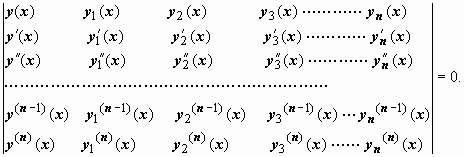  Раскрывая этот определитель по первому столбцу, получим искомое уравнение. Пример: составить линейное уравнение, у которого фундаментальная система решений равна y₁(x) = cos x, y₂(x)= x³. Решение: 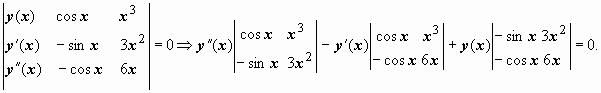  Заметим, что коэффициент при старшей производной оказывается равным вронскиану фундаментальной система решений: 

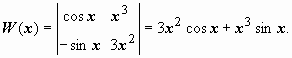
 Дальнейшие преобразования дают 

, или  .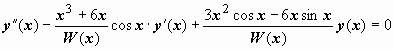

Это и есть искомое уравнение. Его коэффициенты непрерывны на любом интервале, на котором  .

2.2.9. Формула Остроградского-Лиувилля.

Пусть в уравнении y'' + p(x)y' + q(x)y = 0 функции p(x),q(x) непрерывны на [a;b], а

y₁ = y₁(x),y₂ = y₂(x) — решения данного уравнения.

Продифференцировав определитель Вронского получим

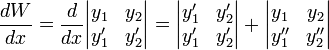
Первое слагаемое равно 0, так как этот определитель содержит 2 одинаковые строки. Подставив

y₁'' = − py₁' − qy₁

y₂'' = − py₂' − qy₂

во второе слагаемое и домножив первую строку на q получим

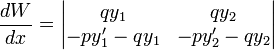
Сложив строки, получим

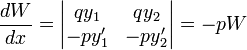
решения линейно независимы, поэтому

 — дифференциальное уравнение с разделяющимися переменными.

Интегрируя, получим

Распишем Вронскиан:

 поэтому

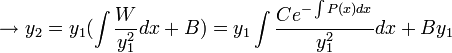
приняв C = 1,B = 0, получим