5. Уравнения в частных производных первого порядка. Методы решения.

Из тетрадки:

ур-е связывающее независимые переменные, искомую фнк и ее частные производные называется ур-ем в частных производных

фнк u=u(x1...xn)

F(x1...xn.u,ux1,...,uxn,u1x1...) = 0 0 ур-е в частных произв.

Utt= a2Uxx <- ур-е колебаний

порядком ДУ называют порядок старшей производной

ОР ДУ в частных произв содержат произвольные фнк

примеры:

U=U(x,y) Ux=0 => U= C(y)

Задача находжения решений УвЧП есть задача нахождения интегральной поверхности

Задача коши состоит в нахождении интегральной поверхности проходящей через заданную кривую

В таком случае З. Коши остается неопределенной для некоторых кривых ч/з которые проходит бесконечно много интегральных кривых

a₁(x1..x_n,u)Du/Dx₁ + .. + a_n(x₁..x_n,u)Du/Dx_n=0 => u=C1

dx₁/a₁(...) = ...= dx_n / a_n( ...)

Ф₁(..) = C₂ .... Ф_n-1(...) =C_n

общее решение выглядит так : U= f(Ф₁(...),...,Ф_n(...))

для неоднородных :

a₁(x₁..x_n,u)Du/Dx₁ + .. + a_n(x₁..x_n,u)Du/Dx_n=B(x₁...x_n,u)

dx₁/a₁(...) = ... = dx_n / a_n( ...) = dU / b(...)

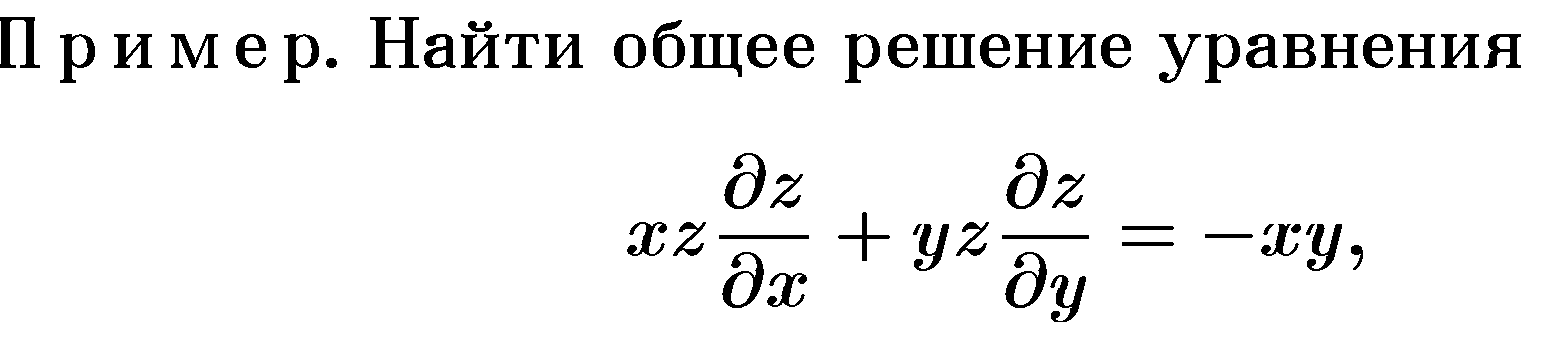
6.1. Классификация уравнений математической физики.

  Классификация уравнений математической физики. Значительная часть У. м. ф. составляют линейные уравнения с частными производными 2-го порядка общего вида:

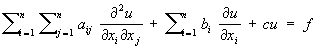   , (1)

  где все коэффициенты a_ij (a_ij = a_ij), b_i, с и правая часть f представляют собой заданные функции независимых переменных x₁, x₂,..., х_п (n > 2), а u – искомая функция тех же аргументов. Свойства решений уравнения (1) существенно зависят от знаков корней (алгебраического относительно л) уравнения

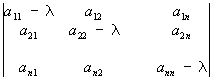    = 0, (2)

  и поэтому классификация уравнений (1) проводится в соответствии с этими знаками. Если все n корней уравнения (2) имеют одинаковый знак, то говорят, что уравнение (1) принадлежит к эллиптическому типу; если один из корней имеет знак, противоположный знаку остальных n – 1 корней, – к гиперболическому типу; наконец, если уравнение (2) имеет один нулевой корень, а прочие корни одинакового знака, – к параболическому типу. Если коэффициенты a_ij постоянны, то уравнение (1) принадлежит к определенному типу независимо от значений аргументов; если же эти коэффициенты зависят от x₁,..., х_п, то и корни уравнения (2) зависят от x₁,..., х_п, а потому уравнение (1) может принадлежать к разным типам при различных значениях аргументов. В последнем случае (уравнение смешанного типа) изучаемая область изменения аргументов состоит из зон, в которых тип уравнения (1) сохраняется. Если корень уравнения (2), переходя от положительных значений к отрицательным, обращается в нуль, то между зонами эллиптичности и гиперболичности расположены зоны параболичности (надо отметить, что и в ряде др. отношений параболического уравнения занимают промежуточное положение между эллиптическими и гиперболическими).

  Для линейных уравнений с частными производными выше 2-го порядка и для систем уравнений с несколькими искомыми функциями классификация более сложна.

6.2. Волновое уравнение

  Волновое уравнение:

  

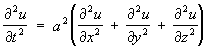
  – простейшее уравнение гиперболического типа, а также соответствующие неоднородные уравнения (в правой части которых добавлены известные функции) – телеграфное уравнение и т.д. Уравнения и системы этого типа появляются при анализе различных колебаний и волновых процессов. Свойства уравнений и систем гиперболического типа во многом аналогичны свойствам приведённых простейших таких уравнений.