2.2.1. Теорема существования и единственности решения для дифференциальных уравнений высших порядков.

если f(x) , p_i(x) - непрерывны на (a,b) a x₀ - тчк этого интервала

то по условию задачи коши ⁽¹⁾y(x₀)=y₀, y'(x₀)=y₀'... y^n-1(x₀) =y₀^n-1

существует фнк определенная на (a,b) и удовлетворяющая условию

Ly= yⁿ + p₁(x)y^n-1 + .... = f(x) и начальными условиям (1)

Ly - линейный оператор

y₁,y₂ - 2 частных решения , Ly=0

тогда y1+ y2 - третье ЧР этого ур-я

док-во

y₁=0

y₂=0

Ly1 + Ly2 = yⁿ + p₁(x) y^n-1 + .... yⁿ + p₁(x) y^n-1 + ....= (y₁+y₂)ⁿ + ... p_n(y₁+y₂) = L(y1+y2) = 0 + 0 = 0 lдоказали что y₁+y₂ - ЧР

Теорема

если y₁ .. y_n - ЧР линура то С*y₁ где С =const - тоже решение этого линура

Следствие

если y₁ .. y_n - ЧР линура то их линейная комбинация y= C₁y₁ + .. +C_ny_n есть решение содержащие произвольные составляющие, если все эти составляющие существенны то это выражение есть общее решение

Замечание

из этих 2х теорем => что L - линейный оператор

!!!!!!

вообще говоря все что касается криво описанного здесь линейного оператора относится к следующему билету... но тогда здесь проме формулировки писать нечего

2.2.2. Линейный оператор и его свойства.

Множество функций, имеющих на интервале (a, b) не менее n производных, образует линейное пространство. Рассмотрим оператор L_n(y), который отображает функцию y(x), имеющую   производных, в функцию, имеющую k - n производных:

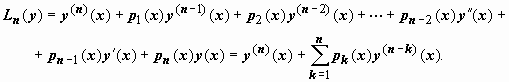
С помощью оператора L_n(y) неоднородное уравнение можно записать так: L_n(y) = f(x);

однородное уравнение примет вид L_n(y) = 0);

Теорема 14.5.2. Дифференциальный оператор L_n(y) является линейным оператором.  Док-во непосредственно следует из свойств производных:  1. Если C = const, то 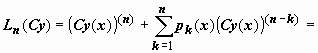 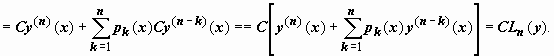  2.   

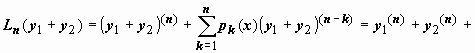
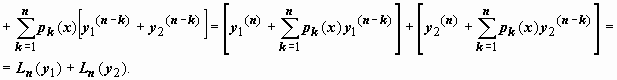
материал стащен с какого то сайта.. все то что рассказывали на лекции можно найти в предыдущем билете в том варианте в каком оно давалось

2.2.3. Определитель Вронского. Линейная зависимость и независимость системы функций.

Определителем Вронского (вронскианом) системы n- 1 раз дифференцируемых функций y₁(x), y₂(x), …, y_n(x) называется определитель

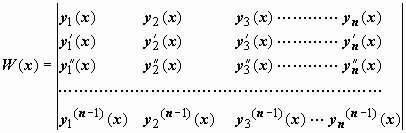
Теорема о вронскиане ЛЗ системы функций. Если система функций y₁(x), y₂(x), …, y_n(x) ЛЗ на интервале (a, b), то вронскиан этой системы тождественно равен нулю на этом интервале. 

Если определитель Вронского W(x) системы y₁(x),y₂(x), …, y_n(x) частных решений ЛОДУ отличен от нуля в некоторой точке  , то W(x) отличен от нуля в любой точке этого интервала. 

Если W(x) - определитель Вронского системы y₁(x),y₂(x), …, y_n(x) частных решений ЛОДУ, то либо   на интервале (a, b) (что означает линейную зависимость этих решений на (a, b)), либо   в любой точке этого интервала (что означает линейную независимость этих решений на (a, b)). 

ЛЗ и ЛНЗ: Система функций y₁(x), y₂(x), …, y_n(x) называется линейно зависимой на интервале (a, b), если существует набор постоянных коэффициентов  , !=0 одновременно, таких, что линейная комбинация этих функций тождественно равна нулю на (a, b):   для  .  Если равенство   для   возможно только при  , система функций y₁(x), y₂(x), …, y_n(x) называется ЛЗ на интервале (a, b).  Другими словами, функции y₁(x), y₂(x), …, y_n(x) ЛЗ на интервале (a, b), если существует равная нулю на (a, b) их нетривиальная линейная комбинация. Функции y₁(x),y₂(x), …, y_n(x) линейно независимы на интервале (a, b), если только тривиальная их линейная комбинация тождественно равна нулю на (a, b).