
- •1.1.. Определение дифференциального уравнения. Понятие общего решения и частного решения.
- •1.2. Уравнения с разделяющимися переменными(УсРп).
- •1.3. Однородные уравнения и уравнения, приводящиеся к однородным.
- •1.4. Линейные уравнения 1-ого порядка(ЛинУры).
- •1.5. Уравнение Бернулли.
- •1.6. Уравнение Риккати.
- •1.7. Уравнения в полных дифференциалах(УвПд)
- •1.8. Уравнения с интегрирующим множителем.
- •1.9. Теорема Коши о существовании и единственности решения задачи дифференциального уравнения 1-ого порядка.
- •1.10. Метод последовательных приближений.
- •1.11. Особые точки и особые решения.
- •1.12. Уравнения, неразрешенные относительно производной.
- •2.1. Уравнения, допускающие понижения порядка.
- •2.2. Линейные дифференциальные уравнения с переменными коэффициентами.
- •2.2.1. Теорема существования и единственности решения для дифференциальных уравнений высших порядков.
- •2.2.2. Линейный оператор и его свойства.
- •2.2.3. Определитель Вронского. Линейная зависимость и независимость системы функций.
- •2.2.4. Свойства решений линейного однородного дифференциального уравнения.
- •2.2.5. Фундаментальная система решений линейного однородного дифференциального уравнения.
- •2.2.6. Теорема о структуре общего решения линейного однородного дифференциального уравнения.
- •2.2.7. Теорема о существовании фундаментальной системы решений линейного однородного дифференциального уравнения.
- •2.2.8. Восстановление линейного однородного уравнения по фундаментальной системе решений.
- •2.2.9. Формула Остроградского-Лиувилля.
- •2.3.1. Линейные уравнения с постоянными коэффициентами.
- •2.3.2.1. Метод подбора частного решения неоднородного уравнения с правой частью специального вида.
- •5. Уравнения в частных производных первого порядка. Методы решения.
- •6.1. Классификация уравнений математической физики.
- •6.2. Волновое уравнение
- •6.3. Телеграфное уравнение,
- •6.4. Уравнение Лапласа,
- •6.5. Уравнение теплопроводности
1.9. Теорема Коши о существовании и единственности решения задачи дифференциального уравнения 1-ого порядка.
(1) y'=f(x,y) (1)
(2) y(x0) = y0 (2)
предположение относительно f(x,y) :
1) f(x,y) - непрерывна в замкнутой области R,
|x-x0| <a
|y-y0| <b , a,b > 0
2) f(x,y) удовлетворяет в области R относительно "у" условию Липшица:
![]() N>0
N>0
![]() (x,y1),(x,y2)
(x,y1),(x,y2)![]() R
: |f(x,y1)
- f(x,y2)|
<= N
|y1-y2|
R
: |f(x,y1)
- f(x,y2)|
<= N
|y1-y2|
N - постоянная Липшица
если выполняются эти 2 предположения то единственное решение y=ф(х) определенного и непрерывного на |x-x0|<n , n=min(a,b/m) /* m<|f| в R */, такое что y(x0)=y0
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
проверить что такое ф(х ) и че это вообще за срань
1.10. Метод последовательных приближений.
(1) y'= f(x,y) (1)
(2) y(x0)=y0 (2)
з аменим
(1) и (2) эквивалентной ей задачей
аменим
(1) и (2) эквивалентной ей задачей
(3)
y(x)=y0
+
![]() f(t,y(t)) dt (3)
f(t,y(t)) dt (3)
Док-во
покажем эквивалентность
y(x) - решение (1) и (2)
dy = f(x,y) dx
воспользуемся условием 2 (каким?????????????)
y(x) = y0 + f(x,y) dx = (3)
обратное док-во
y(x) - решение(3)
под стоит непрерывная фнк рассмотрим по переменному пределу(оО ?????) =>
означает непрерывную и дифф-ую фнк верхнего предела
y'(x)=0 + f(x,y(x)) -> получили (1)
подставим в (3) x->x0
y(x0)=y0 + 0 -> получили (2)
формула последовательного приближения
y1(x) = y0 + f(t,y0(t)) dt
y2(x) = y0 + f(t,y1(t)) dt
yn(x) = y0 + f(t,yn-1(t)) dt - сходится к решения задачи Коши (1),(2)
1.11. Особые точки и особые решения.
Особая
точка
- точка в
![]() окрестности которой нарушается условие
единственности решения
окрестности которой нарушается условие
единственности решения
линия из особой точки - особая линия
если особая линия удовлетворяет ур-ю то она называется особым решением(ОР)
Способы нахождения ОР
1)
находим линии где
![]()
![]() f/
y
f/
y
2) нахождение дискрименантной кривой
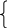 F(x,y,y')=0
F(x,y,y')=0
F(x,y,y') / y' = 0
если такая кривая будет найдена то нужно проверить условие касания
y1(x) = y2(x)
y1'(x) = y2'(x)
3) Ф(x,y,c) =0 - семейство решений
Ф / С =0 - y=ф(х) - огибающая семейство решений
если такая огибающая будет найдена то нужно проверить условие касания
y1(x) = y2(x)
y1'(x) = y2'(x)
фишка этого метода в том что мы имеет решение и можем найти особые решения, не имея исходного уравнения
1.12. Уравнения, неразрешенные относительно производной.
это ДУ в которых нельзя выразить старшую степень производной в одну из частей ур-я
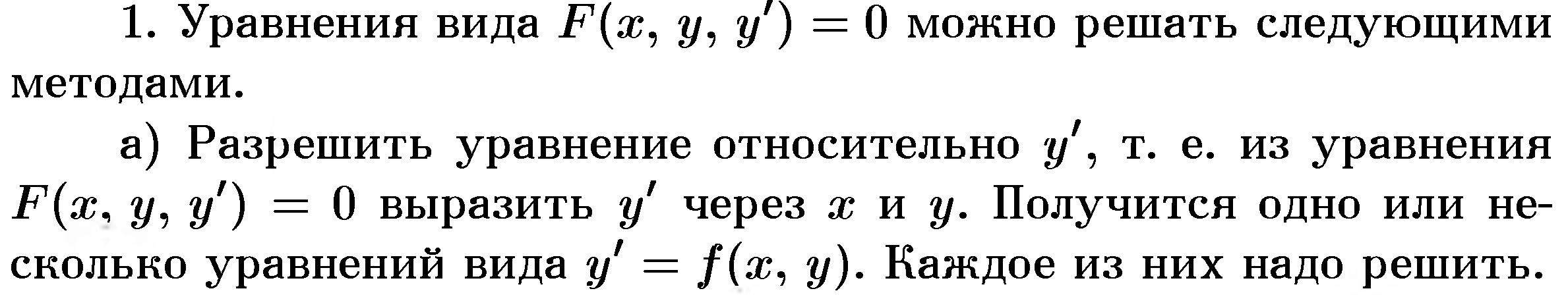
б) метод введения параметра :
p= y' заменяется везде и потом находить р и подставляется в исходное ур-е , что обусловливает получение ответа

ур-я Лагранжа :
y= x*f(y') + k(y')
решаются методом введения параметра
ур-я Клеро :
y= x*y' + k(y')
решаются методом введения параметра
!!!! не забывать проверять ОР и условия касания
2.1. Уравнения, допускающие понижения порядка.


2.2. Линейные дифференциальные уравнения с переменными коэффициентами.
by Филипов: ( но чует моя жопа что это не то)


