1.1.. Определение дифференциального уравнения. Понятие общего решения и частного решения.
ДУ - ур-е связывающее независимую переменную Х, искомую переменную У и ее производные
Порядок ДУ - порядок его старшей производной
(1) если есть переменная от 1 арг. у=у(х) (1) тогда ДУ зовется обыкновенным.
любая фнк у=у(х) которая обращает обыкновенное ДУ в тождество называется решением этого ДУ , а график этой фнк это интегральная кривая
(2) Ф(х,у) =0(2) - зовется интегралом ур-я (1) если каждая фнк у(х) определяемая ур-ем (2) обращает ДУ (1) в тождество и имеет непрерывные производные до n-ого порядка включительно
процесс решения ДУ называют интегрированием
Понятие общего решения и частного решения.
виды ур-й:
f(x,y,y') =0 - не разрешенное относительно У
(1)y'=f(x,y)(1) - разрешенное относительно У
общим решением ур-я (1) зовется фнк y=ф(x,c) удовлетворяющая следущим условиям:
- для любого С фнк ф обращает (1) в тождество
- для любых начальных условий (x0,y0) из области определения фнк f(x,y), существует С* такое что (х,С*) удовлетворяет данным начальным условиям
Существует ровно одна кривая-решение, проходящая через каждую точку с № 0.
Каждое отдельное решение называется частным решением дифференциального уравнения;
если удается найти формулу, содержащую все частные решения (за исключением, быть может, нескольких особых), то говорят, что получено общее решение.
Частное решение представляет собой одну функцию, в то время как общее - целое их семейство.
1.2. Уравнения с разделяющимися переменными(УсРп).
(1) ур-е вида M(x)N(y)dx + P(x)Q(y)dy = 0(1) называется ур-ем с разделяющимися переменными
как решать
ур-е (1) делим на N(y)*P(x) , получим
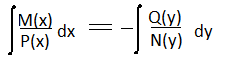
* нужно учитывать что P(x) и N(y) != 0
A*B=0 если A=0 или B=0 при этом другой член произведения существует
берем
x=a
и P(x)=0,
подставляем в (1)=>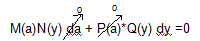
=>
0=0 => х=а - решение
абсолютно аналогично делается с у=b
!!!!в ответе кроме общего решения типа : y=C*x^2 нужно еще проверять многочлены P и N на которые делили, они тоже могут быть решениями ( частными??????????)
ур-я приводящиеся к УсРП
это вида y'=f(ax+b) приводится к ур-ям с раздел. переменными заменой z=ax+b или z=ax+by+c,
где a,b,c - const
z - новая фнк
1.3. Однородные уравнения и уравнения, приводящиеся к однородным.
f(x,y)
= однородное
измерение
А если
t
f(tx,ty)
= t^A
* f(x,y)
ур-е вида y'=f(x,y) - однородное, если f - фнк 0-ого измерения.
f(x,y)=t^0 * f(tx,ty) , t
t=1/x
f(x,y)=f(1,y/x)=ф(y/x)
y'=ф(y/x) - однородное
как решать
y/x=z , y=zx , y'=z'x + z, после подстановки в получится ур-е с разделяющимися переменными
!!!! нельзя забывать что надо дополнительно проверять p(x) и n(y) на равенство нулю( из УсРП)
ур-я приводящиеся к однородным
это
ур-я вида: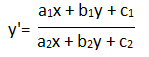
как решать
1)
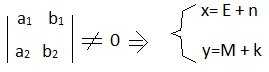где k,n
= const
, такая замена делается чтобы ур-е стало
однородным.
после замены приравняем все константы в числителе и знаменателе к 0 (ex. -2n+4k-6=0 и n+k-3=0), найдем их, подставим обратно в уравнение.
после чего сократим дробь на Е или М и получим однородное ур-е
2)
и решаем его как однородное