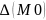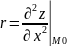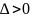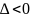8. Производная по направлению, градиент, их свойства и связь (с доказательством), физический смысл.

Пусть 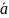- произвольный ненулевой вектор, u=f(x,y,z) – дифференцируемая функция, M0(x0,y0,z0) – точка области определения этой функции. Расссмотрим точку M(x,y,z)  D(f) такую, что вектор 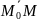коллинеарен вектору

Производная от функции , u=f(М) по направлению в точке М0 - предел , где - расстояние между точками M и М0,

Обозначается , вычисляется по формуле:

,

Где , , 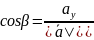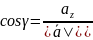- направляющие косинусы вектора

Производная по направлению характеризует скорость изменения функции в направлении заданного вектора: 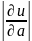определяет величину скорости, знак 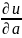- характер изменения (возрастание или убывание).

Применительно к теории поля, производная по направлению позволяет проследить за изменением скалярной величины U(M) при перемещении точки М в каком либо заданном направлении

Градиентом функции , u=f(x,y,z) (скалярного поля) в точке M0(x0,y0,z0) называется вектор, координаты которого равны значениям частных производных 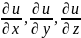, вычисленным в точке М0. Градиент функции u=f(М) обозначается символом grad u(M0)

grad u(M0)=( )

Каждой точке М области определения функции соответствует свой вектор grad u(M), в этом случае говорят, что скалярное поле u=f(М) порождает векторное поле grad u(M)(поле градиента)

Свойства градиента:

• Производная функции u=f(x,y,z) по направлению вектора равна скалярному произведению градиента функции на орт вектора

• Градиент указывает направление наискорейшего роста функции (скалярного поля) в данной точке М0б при этом наибольшая скорость изменения функции в точке равна

max =|grad u|=

• Градиент функции u=f(М) в точке М0 перпендикулярен линии (поверхности) уровня этой функции, проходящей через точку М0

9. Линеаризация функции одной и нескольких переменных, ее геометрическая интерпретация, формула линеаризации.

Если функция u=f(x1,x2,…xn)дифференцируема в точке М0, то при достаточно малых по абсолютному значению приращения аргументов полное приращение функции можно с как угодно малой относительной погрешностью заменить полным дифференциалом этой функции

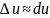
Откуда следует приближенное равенство

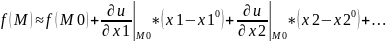- формула лианеризации функции в окрестностях точки М0

Позволяет заменить дифференцируемую в окрестностях точки М0 функцию заменить приближенно равной ей линейной функцией

С геометрической точки зрения означает замену поверхности z=f(x,y) в окрестности точки М0 касательной плоскостью, проведенной к поверхности в этой точке

10. Неявная функция 1-й, 2-х, 3-х и т.д. переменных. Дифференцирование неявных функций. Примеры для функций 1-й, 2-х, 3-х переменных.

F(x,y,z,u)=0 – функция u, заданная неявно

– функция 3-х переменных

11. Определение точек максимума и минимума ФНП, экстремумов ФНП.

Пусть D – область определения функции z=f(M).

Точка М0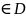 называется точкой максимума функции z=f(M), а значение f(M0) называется максимумом этой функции, если существует окрестность точки М0, такая, что для любой точки М≠М0 из этой окрестности выполняется равенство f(M0)>f(M)

Если f(M0)<f(M) – точка минимума

Точки максимума и минимума функции называют точками экстремума, а значения функции в этих точках называются экстремумами этой функции

12. Необходимое условие существования экстремума, критические точки, их связь с точками экстремума.

Если функция z=f(M) в точке М0 имеет экстремум, то в этой точке частные производные первого порядка функции z=f(M) по каждому из ее аргументов либо равны нулю, либо не существуют. Точки, в которых эти условия выполняются, называются критическими точками функции (точками возможного экстремума)

13. Достаточное условие существования экстремума ФНП, частный случай функции 2-х переменных.

Пусть функция u=f(x1,x2,…xn) дважды непрерывно дифференцируема в окрестности критической точки М0, а 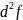– ее дифференциал второго порядка. Если для любых, не равных одновременно нулю значений x1,x2… ,

• в точке М0 имеет постоянный знак, то М0 – точка экстремума функции u=f(x1,x2,…xn), причем:

  • Если (М0)<0 – точка максимума

  • Если (М0)>0 – точка минимума

• в точке М0 принимает как положительные, так и отрицательные значения, то М0 не является точкой экстремума

Для 2-х переменных :

Пусть и М0 – критическая точка функции z=f(x,y). Тогда

условия		Наличие и вид экстремума
	r>0	М0- точка минимума
	r<0	М0- точка максимума
	Произвольного знака	В точке М0 нет экстремума
	Произвольного знака	Нужны дополнительные исследования