29. Гармонические электромагнитные колебания и их характеристики. Электрический колебательный контур. Дифференциальное уравнение собственных гармонических колебаний и его решение.

Колебания называются гармоническими, если некоторая величина, характеризующая это колебание, изменяется по закону cos или sin, т. е. имеет вид:

или ,

где х — значение изменяющейся величины, t — время, остальные параметры — постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний,   — полная фаза колебаний,   — начальная фаза колебаний.

Это замкнутая электрическая цепь, в которую включены катушка индуктивности и конденсатор. Колебательный контур — это своего рода «электрический маятник»— основа многих радиотехнических устройств. Он задает или определяет частоту колебаний тока.

Чтобы в контуре возникли электрические колебания, его нужно «подтолкнуть»— зарядить конденсатор от какого-либо источника тока, например от батареи, а затем соединить заряженный конденсатор с катушкой индуктивности. С этого момента конденсатор начнет разряжаться через катушку, создавая в колебательном контуре нарастающий электрический ток, а вокруг витков катушки — магнитное поле. Когда конденсатор полностью разрядится, ток через катушку достигнет максимального значения и магнитное поле скажется наиболее сильным — электрический заряд конденсатора преобразовался в магнитное поле катушки. Ток в контуре некоторое время будет идти в том же направлении, но уже за счет убывающей энергии магнитного поля, накопленной катушкой, а конденсатор начнет перезаряжаться. Как только магнитное пате катушки исчезнет, ток в контуре на мгновение прекратится. К этому моменту конденсатор окажется полностью перезаряженным, поэтому через катушку вновь потечет ток, но уже в противоположном направлении. В результате в контуре возникают колебания электрического тока, продолжающиеся до тех вор, пока вся энергия, запасенная конденсатором, не израсходуется на преодоление сопротивления провода катушки индуктивности. Изменяя индуктивность (число витков) катушки и емкость конденсатора, можно в широких пределах изменять частоту колебаний в контуре. Электрические колебания, возбужденные з контуре зарядом конденсатора, свободные, а следовательно, затухающие.

Пусть конденсатор ёмкостью C заряжен до напряжения  . Энергия, запасённая в конденсаторе, составляет:

Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна , где   — индуктивность катушки,   — максимальное значение тока.

Обобщенное гармоническое колебание в дифференциальном виде

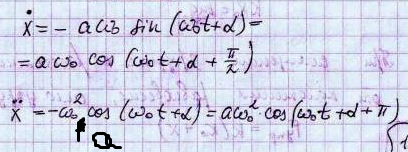
Любое нетривиальное решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой 

30. Затухающие электромагнитные колебания. Дифференциальное уравнение и его решение. Логарифмический декремент.

Затухающие электромагнитные колебания - это свободные электромагнитные колебания в реальном колебательном контуре, представляющем собой последовательное соединение катушки индуктивности L, конденсатора емкости С и электрического сопротивления R.

Свободные затухающие колебания линейной системы описываются уравнением:

Это дифференциальное уравнение, где   - коэффициент затухания,   - собственная частота системы, т.е. частота, с которой совершались бы колебания в отсутствии затухания.

Решение рассмотрим в виде где u=u(t).Далее находим вторую производную и получаем Решение этого уравненияя зависит от знака коэффициента перед искомой величиной. Рассмотрим случай, когда этот коэффициент положителен.  Тогда получим уравнение, решением которого является функция x=А₀cos(wt+j), следовательно, решение уравнения в случае малых затуханий: где s=x(t), а Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины. Тогда период затухающих колебаний равен Если A(t) и А(t + Т) ≈ амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение называется декрементом затухания, а его логарифм называется логарифмическим декрементом затухания.