47 Дифференциалы высших порядков. Формула Тейлора для функции нескольких переменных.

48 Дифференцирование сложных функций . Полная производная.

Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных.

Одномерный случай

Пусть даны функции, определённые в окрестностях на числовой прямой , где y0 = f(x0), и Пусть также эти функции дифференцируемы: Тогда их композиция также дифференцируема: и её производная имеет вид:

Замечание

В обозначениях Лейбница цепное правило для вычисления производной функции, где x = x(t), принимает следующий вид:

Инвариантность формы первого дифференциала

Дифференциал функции z = g(y) в точке y0 имеет вид:

где dy — дифференциал тождественного отображения :

Пусть теперь Тогда , и согласно цепному правилу:

Таким образом форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли независимая переменная функцией или нет.

Пример

Пусть h(x) = (3x2 − 5x)7. Тогда функция h может быть записана в виде композиции где

Дифференцируя эти фунем(сам не знаю что за слово)))

49Дифференцирование сложных функций . Общий случай (Вычисление двойного интеграла в декартовых координатах)

Область D называется правильной относительно оси Ох, если прямая, параллельная этой оси, проходящая через внутреннюю точку области D, пересекает границу области в двух точках. Аналогично определяется правильная область относительно оси Оу.

Рисунок 2. Рисунок 3.

Рисунок 2 - Область, правильная, относительно оси Оу Рисунок 3 - Область, правильная, относительно оси Ох

Область D, правильную относительно как Ох, так и Оу, называют просто правильной областью.

Если область D - правильная относительно Оу (рисунок 2), двойной интеграл вычисляется по формуле:

Правую часть формулы (8) называют повторным (двукратным) интегралом. Вычисление повторного интеграла начинаем с вычисления внутреннего интеграла.

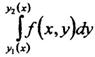
в котором переменную х надо принять при интегрировании за постоянную величину. После подстановки пределов интегрирования в первообразную получаем некоторую функцию, зависящую от х, которую затем интегрируем на отрезке [a,b].

Если область D является правильной относительно оси Ох (рисунок 3), двойной интеграл вычисляется по формуле:

Если область D - просто правильная, можно применять как формулу (8), так и формулу (9). При этом переход от одной формулы к другой называют изменением порядка интегрирования.

Сам процесс перехода от двойного интеграла к повторному и расстановка пределов интегрирования для внешнего и внутреннего интегралов называют приведением двойного интеграла к повторному.

Правило расстановки пределов.

В пределах внутреннего интеграла (интеграла по первой переменной) в общем случае стоят функции второй переменной.

В пределах внешнего интеграла (по второй переменной) стоят постоянные числа. В результате вычисления двойного интеграла получается некоторое постоянное число.

Если область не является правильной ни относительно оси Ох, ни относительно оси Оу, её разбивают на конечное число областей , правильных относительно одной из осей и при вычислении применяют свойство 2.

Пример 1.

Вычислить двойной интеграл

двумя способами, если граница области D задана уравнениями:

Решение 1, а

Построив кривые, получим область D (рисунок 4). Область правильная. Применим формулу (8). При этом уравнение верхней границы области х=у2 преобразуем к виду :

Рисунок 4.- область интегрирования к примеру 1,а

Рисунок 5.- область интегрирования к примеру 1,b

Изменим порядок интегрирования и применим формулу (9):

Решение 1, b

Область D построена на рисунке 5. Область D правильная. Выбираем для интегрирования формулу (9):

Изменим порядок интегрирования. При этом нижняя граница области D задана двумя аналитическими выражениями . В этом случае область D нужно разбить на две области Dl, D2 с помощью прямой, проходящей по оси Оу. На основании свойства 2 двойного интеграла получаем:

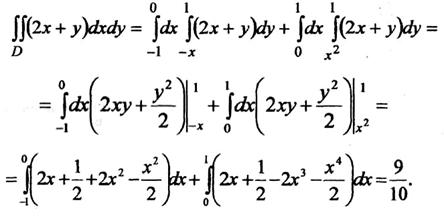
Вычислить несобственный интеграл или установить его расходимость.

Решение. Так же, как и в предыдущем примере, перейдем от несобственного интеграла к определенному под знаком предела.

Замечание: когда , то .

Поэтому получаем, что , а это значит, что данный интеграл расходится.