Для определённого интеграла

В целом аналогично случаю неопределённого интеграла:

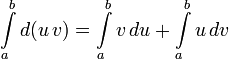
30.Интеграл и площадь

С точки зрения геометрии определенный интеграл – это ПЛОЩАДЬ.  То есть,  определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры. 

Площадь криволинейной трапеции численно равна определенному интегралу 

 Если Вам предложено найти площадь фигуры с помощью определенного интеграла, то площадь всегда положительна! Поэтому иногда перед интегралом стоит минус.

31. Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. В полярных координатах площадь сектора, ограниченного дугой кривой    и лучами   и  , выражается интегралом   .

32. Длина дуги   радиуса   вычисляется по формуле

; где   — центральный угол в радианах

; где   — центральный угол в градусах:

33. Пусть уравнение кривой L в полярных координатах 

 причем функция  непрерывно дифференцируе-

ма на [а,b]. Используя формулы перехода от полярных координат к декартовым и принимая за параметр угол   имеем параметрические уравнения кривой   Тогда

   

34.Вычисление объема тела по известным площадям его параллельных сечений.

 

 

 

 

 

 

 

  Пусть имеется тело объема V. Площадь любого поперечного сечения тела Q, известна как непрерывная функция Q = Q(x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки х_i разбиения отрезка [a, b]. Т.к. на каком- либо промежуточном отрезке разбиения [x_i-1, x_i] функция Q(x) непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно M_i и m_i.

  Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны M_ix_i и m_ix_i здесь x_i = x_i - x_i-1.

  Произведя такие построения для всех отрезков разбиения, получим цилиндры, объемы которых равны соответственно   и  .

  При стремлении к нулю шага разбиения , эти суммы имеют общий предел:

Таким образом, объем тела может быть найден по формуле:

35. Объем тел вращения.

 

  Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [a, b]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения.

 

 y = f(x)

 Т.к. каждое сечение тела плоскостью x = const представляет собой круг радиуса  , то объем тела вращения может быть легко найден по полученной выше формуле:

36.Бесконечные пределы интегрирования

Если функция   определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:

, где с — произвольное число.

Одним из основных результатов математического анализа является теорема Ньютона – Лейбница П усть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда 

37. Несобственный интеграл от разрывной функции

     Пусть функция f(x) непрерывна при a ≤ x < b и имеет точку разрыва при x = b. Тогда соответствующий несобственный интеграл от разрывной функции определяется формулой

     (8)

и называется сходящимся или расходящимся в зависимости от того, существует или не существует предел правой части равенства (8).

Одним из основных результатов математического анализа является теорема Ньютона – Лейбница П усть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда 

38.

Определение-переменная z называется функцией двух переменных x и y,если по некоторому закону каждой паре,из некотого множества ставится в соответствие вполне определенное значение z.Обозначение z=f(x,y) можно наглядно изобразить с помощью некоторой поверхности в простраственной прямоугольной системе координат.

Функции. Область определения. Способы задания

О: Функцией , которая определена на множестве  и принимает значения на множестве , именуется такое соответствие между этими множествами, когда для каждого существует единственный элемент : .

Множество является областью определения функции; - областью значений функции;  является независимой переменной (аргументом); является зависимой переменной (функцией).

На языке геометрии функция показывает множество на множестве : , тогда - обра ,  - образ .

Пример: Функция  .

Если каждому значению соответствует несколько или сколь угодно много значений , то считается, что задана многозначная функция. При анализе подобных функции выбирают промежутки, где они однозначны. Чаще всего используются три способа задания функции: аналитический, графический, табличный.

При использовании аналитического способа функция задаётся одной или несколькими формулами, которые действуют на непересекающихся частях области определения.

При использовании графического способа функция задаётся посредством кривой (графика) в плоскости , при этом любая прямая, которая параллельна оси , пересекает кривую не более чем в одной точке.

Если функция задана аналитическим способом, то её график представляется возможным построить. К примеру, функция имеет график, который показан на рис. 6.1.

При табличном способе задания существует таблица значений аргумента и соответствующих значений функции.

Рис. 6.1

О: Функция именуется возрастающей на , если большему значению аргумента соответствует большее значение функции: , если .

Функция только возрастающая или убывающая на именуется монотонной.

Рассмотрим функцию  где М(х,у)или

О: Множество D точек М пространства (или ) вместе с соответствующими этим точкам числами, которые определяются функцией u(М), называется скалярным полем (СП), а функция — функцией поля.

Если то СП является плоским, если— пространственным.

Примерами СП являются поле распределения температуры в данном теле, поле распределения электрического потенциала в пространстве вокруг электрического заряда и т.п.

СП функции не зависит от времени Такое поле называется стационарным. Геометрически СП изображается на плоскости линиями уровня где с — значение

 в пространстве — поверхностями уровня (x,y,z) = с.

Примеры: 1) уравнения линий уровня: (рис. 28.1).

2) уравнения поверхностей уровня: — семейство параболоидов вращения с осью вращения  OZ и вершинами, расположенными на OZ (рис. 28.2).

Рис. 28.1

Окре́стность точки — множество, содержащее данную точку, и близкие (в каком-либо смысле) к ней.

На пример, если мы имеем множество нечетных чисел 1,3,5,7,9,...27,29,... То окрестностью точки 5 можно считать множество состоящеее из  3,5,7

39. Предел функции нескольких переменных

Предел функции нескольких переменных

Пусть функция n переменных u = f(x) = f(x₁, x₂,  … , x_n) определена в некоторой окрестности точки a = (a₁, a₂,  … , a_n)  Rⁿ , за исключением, быть может, самой точки a.

Определение 1. Число A называется пределом функции f(x) в точке a = (a₁, a₂,  … , a_n), если

ε > 0   δ _ε > 0 :    x  O_δ(a)  |f(x) − A| < ε

Обозначение: 

lim

x → a

 f(x) = A.

В пространстве R² предел функции f(x,y) в точке a(a₁, a₂) принято обозначать следующим образом:

lim

x → a1 y → a2

  f(x, y) = A.     или     

lim

x → a1 y → a2

  f(x, y) = A.

Замечания.

Определение предела функции n переменных в точности совпадает с определением предела функции одной переменной, только окрестность точки a теперь не интервал (a − δ, a + δ), а n–мерный открытый шар

(x₁ − a₁)² + (x₂ − a₂)² + … + (x_n − a_n)²   < δ².

Если a — граничная точка области определения D(f) функции f, то определение предела уточняется следующим образом (аналогично понятию одностороннего предела функции одной переменной):

ε >0    δ_ε > 0:   x  O_δ(a) ∩ D(f)  |f(x) − A|<ε.

Теорема 1. Пусть функции n переменных f(x) и g(x), определены в области D  Rⁿ и для некоторой точки a

lim

x → a

 f(x) = A  и   

lim

x → a

 g(x) = B.

Тогда

lim

x → a

 [f(x) + g(x)] = A + B,    

lim

x → a

 f(x) · g(x) = A · B,    и при B ≠ 0   

lim

x → a

 

f(x)

g(x)

 = 

A

B

 .

Теорема доказывается так же, как для функции одной переменной.

Определение 2. Функция f(x) называется бесконечно малой в точке a, если 

lim

x → a

 f(x) = 0.

Определения и теоремы о бесконечно малых функций одной переменной справедливы для бесконечно малых функций нескольких переменных.

40.Непрерывность функций нескольких переменных.Свойства непрерывных функций.Точки,линии и поверхности разрыва

Непрерывность функции нескольких переменных

Пусть функция n переменных u = f(x) = f(x₁, x₂,  … , x_n) определена в некоторой окрестности точки a = (a₁, a₂,  … , a_n) О Rⁿ (включая саму точку a).

Определение 1. Функция u = f(x) называется непрерывной в точке a, если

lim x → a  f(x) = f(a).

Обозначим приращения аргументов символами Δx₁ = x₁ − a₁, Δx₂ = x₂ − a₂,  …, Δx_n = x_n − a_n. Соответствующее приращение функцииu=f(x)

Δu = f(a1 + Δx1, a2 + Δx2,   … ,  an + Δxn) − f(a1,  a2,  … ,  an).

называется полным приращением функции u=f(x) в точке a, соответствующим прирашению Δx = {Δx₁, Δx₂,  …, Δx_n}.

Условие, определяющее непрерывную функцию u = f(x) в точке a эквивалентно условию

lim Δx → 0  Δu = 0.

Приращение

δxku = f(a1,  … , ak + Δxk,  … , an) − f(a1, a2,  … , an)

называется частным приращением функции u в точке a, соответствующим приращению Δx_k аргумента x_k.

Определение 2. Функция u = f(x) = f(x₁, x₂,  … , x_n) называется непрерывной в точке a = (a₁, a₂,  … , a_n) по переменной x_k , если

lim Δxk → 0  δxku = 0.

Теорема 1. Если функция u = f(x) = f(x₁, x₂,  … , x_n) непрерывна в точке a, то она непрерывна в этой точке по каждой переменнойx₁, x₂,  … , x_n .

Обратное утверждение неверно.

Теорема 2. Пусть функции f(x) и g(x) , определены в области D М Rⁿ и непрерывны в точке a = (a₁, a₂,  … , a_n) О D .

Тогда функции f(x) + g(x) , f(x) · g(x) и f(x)/g(x) (при g(a) ≠ 0) непрерывны в точке a

Доказательство получается из определения непрерывности функции в точке и теоремы о пределах суммы, произведения и частного двух функций.

Теорема 3. Всякая элементарная функция нескольких переменных непрерывна на множестве, на котором она определена.

Теоремы о свойствах функции одной переменной, непрерывной на отрезке, справедливы для функции нескольких переменных, непрерывной на замкнутом ограниченном множестве (компакте):

Теорема 4. Функция, непрерывная на замкнутом ограниченном множестве, ограничена на этом множестве.

Теорема 5 (Вейерштрасс). Функция, непрерывная на замкнутом ограниченном множестве, достигает на этом множестве своего наибольшего и наименьшего значений.

Свойства

Локальные

Функция, непрерывная в точке  , является ограниченной в некоторой окрестности этой точки.

Если функция   непрерывна в точке   и   (или  ), то   (или  ) для всех  , достаточно близких к  .

Если функции   и   непрерывны в точке  , то функции   и   тоже непрерывны в точке  .

Если функции   и   непрерывны в точке   и при этом  , то функция   тоже непрерывна в точке  .

Если функция   непрерывна в точке   и функция   непрерывна в точке  , то их композиция   непрерывна в точке  .

Глобальные

Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.

Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.

Областью значений функции  , непрерывной на отрезке  , является отрезок   где минимум и максимум берутся по отрезку  .

Если функция   непрерывна на отрезке   и   то существует точка   в которой  .

Если функция   непрерывна на отрезке   и число   удовлетворяет неравенству   или неравенству   то существует точка   в которой  .

Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.

Монотонная функция на отрезке   непрерывна в том и только в том случае, когда область ее значений является отрезком с концами   и  .

Если функции   и   непрерывны на отрезке  , причем   и   то существует точка   в которой   Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.

имеет разрыв при x=a

Классификация точек разрыва функции

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.  Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке

Существуют левосторонний предел   и правосторонний предел  ;

Эти односторонние пределы конечны.