
- •Свойства неопределенных интегралов
- •Тригонометрическая и показательная формы
- •Теорема Безу
- •Доказательство.
- •Теорема о разложении многочлена на линейные множители
- •Определение
- •Примеры
- •[Править]Конечные поля
- •Метод разложение числителя
- •Для определённого интеграла
- •41. Свойства функций, непрерывных в ограниченной и замкнутой области.
- •42 Частные производные, их геометрический смысл.
- •43 Частные производные высших порядков . Теорема о независимости смешанных производных от порядка дифференцирования.
- •44 Касательная плоскость к поверхности, определяемой графиком функции двух переменных . Её уравнение и нормаль к поверхности.
- •45 Полный дифференциал. Достаточное условие дифференцируемости. Свойства полного дифференциала
- •46 Геометрический смысл дифференциала. Применение полного дифференциала в приближенных вычислениях.
- •47 Дифференциалы высших порядков. Формула Тейлора для функции нескольких переменных.
- •48 Дифференцирование сложных функций . Полная производная.
- •49Дифференцирование сложных функций . Общий случай (Вычисление двойного интеграла в декартовых координатах)
- •50 Неявные функции одной переменной . Их дифференцирование
- •52 Уравнение касательной к кривой, задаваемой неявной функцией
- •53 Уравнение касательной плоскости к поверхности, задаваемой неявной функцией
- •54 Экстремум функций нескольких переменных. Необходимые и достаточные условия.
- •55 Нахождение наибольших и наименьших значений функции нескольких переменных.
Метод разложение числителя
Пример 1
Найти
неопределенный интеграл. Выполнить
проверку.
![]()
На уроке Неопределенный интеграл. Примеры решений мы избавлялись от произведения функций в подынтегральном выражении, превращая её в сумму, удобную для интегрирования. Оказывается, что иногда в сумму (разность) можно превратить и дробь!
Анализируя
подынтегральную функцию, мы замечаем,
что и в числителе и в знаменателе у нас
находятся многочлены первой степени: ![]() и
и ![]() .
.
Когда в числителе и знаменателе находятся многочлены одинаковой степени, то помогает следующий искусственный приём: в числителе мы должны самостоятельно организовать такое же выражение, что и в знаменателе:
![]()
Рассуждение может быть следующим: «В числителе мне надо организовать , но если я прибавлю к «иксу» тройку, то, для того, чтобы выражение не изменилось – я обязан эту же тройку и вычесть».
Теперь можно почленно разделить числитель на знаменатель:
![]()
В результате мы добились, чего и хотели. Используем первые два правила интегрирования:

Готово. Проверку при желании выполните самостоятельно.
Обратите
внимание, что ![]() во
втором интеграле – это «халявная»
сложная функция, об особенностях ее
интегрирования я рассказал на уроке Метод
замены переменной в неопределенном
интеграле.
во
втором интеграле – это «халявная»
сложная функция, об особенностях ее
интегрирования я рассказал на уроке Метод
замены переменной в неопределенном
интеграле.
Кстати,
рассмотренный интеграл можно решить и
методом замены переменной, обозначая ![]() ,
но запись решения получится значительно
длиннее
,
но запись решения получится значительно
длиннее
Пример 2
Найти
неопределенный интеграл. Выполнить
проверку.
![]() Это
пример для самостоятельного решения.
Следует заметить, что здесь метод замены
переменной уже не пройдёт.
Это
пример для самостоятельного решения.
Следует заметить, что здесь метод замены
переменной уже не пройдёт.
Внимание, важно! Примеры №№1,2 являются типовыми и встречаются часто. В том числе, подобные интегралы нередко возникают в ходе решения других интегралов, в частности, при интегрировании иррациональных функций (корней).
Рассмотренный приём работает и в случае, если старшая степень числителя, больше старшей степени знаменателя.
Пример 3
Найти
неопределенный интеграл. Выполнить
проверку.
![]()
Начинаем подбирать числитель.
Алгоритм подбора числителя примерно такой:
1)
В числителе мне нужно организовать ![]() ,
но там
,
но там ![]() .
Что делать? Заключаю
в
скобки и умножаю на
:
.
Что делать? Заключаю
в
скобки и умножаю на
: ![]() .
.
2)
Теперь пробую раскрыть эти скобки, что
получится? ![]() .
Хмм… уже лучше, но никакой двойки
при
изначально
в числителе нет. Что делать? Нужно
домножить на
.
Хмм… уже лучше, но никакой двойки
при
изначально
в числителе нет. Что делать? Нужно
домножить на ![]() :
:
![]()
3)
Снова раскрываю скобки: ![]() .
А вот и первый успех! Нужный
получился!
Но проблема в том, что появилось лишнее
слагаемое
.
А вот и первый успех! Нужный
получился!
Но проблема в том, что появилось лишнее
слагаемое ![]() .
Что делать? Чтобы выражение не изменилось,
я обязан прибавить к своей конструкции
это же
.
Что делать? Чтобы выражение не изменилось,
я обязан прибавить к своей конструкции
это же ![]() :
:
![]() .
Жить стало легче. А нельзя ли еще раз в
числителе организовать
.
Жить стало легче. А нельзя ли еще раз в
числителе организовать ![]() ?
?
4)
Можно. Пробуем: ![]() .
Раскрываем скобки второго слагаемого:
.
Раскрываем скобки второго слагаемого:
![]() .
Простите, но у меня вообще-то было на
предыдущем шаге
.
Простите, но у меня вообще-то было на
предыдущем шаге ![]() ,
а не
,
а не ![]() .
Что делать? Нужно домножить второе
слагаемое на
:
.
Что делать? Нужно домножить второе
слагаемое на
:
![]()
5)
Снова для проверки раскрываю скобки во
втором слагаемом:
![]() .
Вот теперь нормально: получено
.
Вот теперь нормально: получено ![]() из
окончательной конструкции пункта 3! Но
опять есть маленькое «но», появилось
лишнее слагаемое
из
окончательной конструкции пункта 3! Но
опять есть маленькое «но», появилось
лишнее слагаемое ![]() ,
значит, я обязан прибавить к своему
выражению
,
значит, я обязан прибавить к своему
выражению ![]() :
:
![]()
Если
всё выполнено правильно, то при раскрытии
всех скобок у нас должен получиться
исходный числитель подынтегральной
функции. Проверяем:
![]() Гуд.
Гуд.
Таким
образом:

Готово. В последнем слагаемом я применил метод подведения функции под дифференциал.
Если
найти производную от ответа и привести
выражение к общему знаменателю, то у
нас получится в точности исходная
подынтегральная функция ![]() .
Рассмотренный метод разложения
в
сумму – есть ни что иное, как обратное
действие к приведению выражения к общему
знаменателю.
.
Рассмотренный метод разложения
в
сумму – есть ни что иное, как обратное
действие к приведению выражения к общему
знаменателю.
Алгоритм подбора числителя в подобных примерах лучше выполнять на черновике. При некоторых навыках будет получаться и мысленно. Припоминаю рекордный случай, когда я выполнял подбор для 11-ой степени, и разложение числителя заняло почти две строчки Вёрда.
Помимо алгоритма подбора можно использовать деление столбиком многочлена на многочлен, но, боюсь, объяснения займут еще больше места, поэтому как-нибудь в другой раз.
24.
25.
Теорема об интегрировании неравенств.
Если в любой точке ![]() выполняется
неравенство
выполняется
неравенство ![]() ,
и функции f(x), g(x) интегрируемы
по отрезку [a,b], то
,
и функции f(x), g(x) интегрируемы
по отрезку [a,b], то  .
.
![]() Док-во.
Для любого разбиения отрезка и любого
выбора точек
Док-во.
Для любого разбиения отрезка и любого
выбора точек ![]() при
при ![]()
 .
Переходя в этом неравенстве к пределу
при
.
Переходя в этом неравенстве к пределу
при ![]() ,
получаем требуемое неравенство.
,
получаем требуемое неравенство.
Среднее значение
Теорема
5.
Если f(x)
- непрерывная функция, заданная на
промежутке [a, b],
то существует такая точка ![]()
![]() ,
что
,
что

 (14)
(14)
В самом деле, пусть M и m наибольшее и наименьшее значения f(x) на промежутке [a, b]. Составим для f(x) какую-нибудь интегральную сумму
![]()
![]()
![]()
Так как при всех k будет m ≤ f(ξk) ≤ M, а xk+1 > xk, то m(xk+1 - xk) ≤ M(xk+1 - xk). Складывая такие неравенства и замечая, что
![]()
![]()
![]()
получим:
m(b - a) ≤ σ ≤ M(b - a).
Переходя в этом неравенстве к пределу при λ → 0, приходим после деления на b - a к новому неравенству
![]()
![]()
![]()
Таким образом, частное
![]()
![]()
![]()
есть число, лежащее между наибольшим и наименьшим значениями непрерывной функции. Как известно, тогда и само это число должно являться одним из значений той же функции. Поэтому в [a, b] обязательно существует такая точка ξ, что h = f(ξ), а это равносильно равенству (14).
Заметим, что равенство (14) справедливо не только при a < b, но и при a = b (тогда обе части этого равенства нули), а также и при a > b (этот случай приводится к рассмотренному изменением знаков). В первом из этих случаев будет ξ = a, а во втором a ≥ ξ ≥ b.
Теорему 5 обычно называют теоремой о среднем значении. Из нее вытекает ряд свойств интеграла, выражающихся неравенствами.
26. Производная интеграла с переменным верхним пределом
Производная интеграла с переменным верхним пределом |
Если
в определенном интеграле Обозначим
верхний предел x,
а переменную интегрирования, чтобы
не смешивать ее с верхним пределом,
обозначим t.
Таким образом, интеграл с переменным
верхним пределом является функцией
от x: Имеет
место теорема: производная
интеграла с переменным верхним пределом
от непрерывной функции равна
подынтегральной функции, в которой
переменная интегрирования заменена
верхним пределом: Доказательство. По определению производной
Тогда Это
значит, что интеграл с переменным
верхним пределом |
27.Формула ньютона-лейбница
Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.
-
Если
 непрерывна
на отрезке
непрерывна
на отрезке  и
и  —
ее любая первообразная на этом
отрезке, то имеет место равенство
—
ее любая первообразная на этом
отрезке, то имеет место равенство
28.Замена переменной в определенном интеграле
При вычислении определенных интегралов с использованием формулы Ньютона-Лейбница предпочтительно жестко не разграничивать этапы решения задачи (нахождение первообразной подынтегральной функции, нахождение приращения первообразной). Такой подход, использующий, в частности, формулы замены переменной и интегрирования по частям для определенного интеграла, обычно позволяет упростить запись решения.
ТЕОРЕМА.
Пусть функция φ(t) имеет непрерывную
производную на отрезке [α,β], а=φ(α), в=φ(β)
и функция f(х) непрерывна в каждой точке
х вида х=φ(t), где t![]() [α,β].
[α,β].
Тогда справедливо следующее равенство:

Эта формула носит название формулы замены переменной в определенном интеграле.
Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным). При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t уравнений φ(t)=а и φ(t)=в. На практике, выполняя замену переменной, часто начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменной t упрощается: α=ψ(а), β=ψ(в).
Пример
19. Вычислить 
Положим
t=2-х2.
Тогда dt=d(2-х2)=(2-х2)'dx=-2xdx
и xdx=-![]() dt.
Если х=0, то t=2-02=2,
и если х=1, то t=2-12=1.
Следовательно:
dt.
Если х=0, то t=2-02=2,
и если х=1, то t=2-12=1.
Следовательно:

29.Интегрирование по частям
Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы
для определённого:

Предполагается,
что нахождение интеграла ![]() проще,
чем
проще,
чем ![]() .
В противном случае применение метода
неоправдано.
.
В противном случае применение метода
неоправдано.

 изменять
верхний предел b,
то будет меняться и значение интеграла,
то есть интеграл будет функцией
верхнего предела.
изменять
верхний предел b,
то будет меняться и значение интеграла,
то есть интеграл будет функцией
верхнего предела.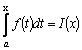 .
.
 где
где  [первый
интеграл представим в виде суммы двух
интегралов, пользуясь свойством
аддитивности]=
[первый
интеграл представим в виде суммы двух
интегралов, пользуясь свойством
аддитивности]=