53 Уравнение касательной плоскости к поверхности, задаваемой неявной функцией

http://vv-usov.narod.ru/mathematical_analysis/implicitsurface/implicitsurface.html

54 Экстремум функций нескольких переменных. Необходимые и достаточные условия.

55 Нахождение наибольших и наименьших значений функции нескольких переменных.

Для того чтобы найти наибольшее и наименьшее значение функции z = f ( x, y) в заданной замкнутой области D, надо:

вычислить первые частные производные;

решив систему (4.17), найти координаты стационарных точек и, если они принадлежат области D, вычислить значение функции в этих точках;

найти наибольшее и наименьшее значение функции на границе D;

из всех найденных значений функции выбрать наибольшее и наименьшее.

Если координаты стационарных точек не принадлежат заданной области D, то наибольшее и наименьшее значение функции лежит на границе.

Пример. Найдем наибольшее и наименьшее значение функции

z = x2 - xy + y2 - 4x

Область D определена линиями:

x = 0, y = 0, 2x + 3y - 12 =0

Найдём координаты стационарных точек:

Построим для наглядности границу D на плоскости XOY.

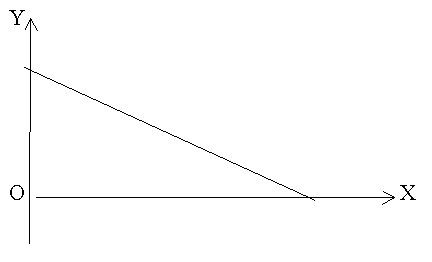
Найденная стационарная точка M (8/3;4/3) принадлежит заданной области D:

Найдём значения функции на границах:

Экстремальная точка на той части границы, которая совпадает с осью OY, лежит на нижней границе интервала. Значение функции в этой точке z (0;0)=0.

На другом конце интервала z (0;4)=16:

– точка экстремума функции на второй границе.

На этой границе, совпадающей с осью OX, вычислим значение функции в трёх точках: (0,0); (2,0); (6,0) – правая граница интервала. В первой точке значение функции уже известно из пункта (а): z(2,0)= -4; z(6,0)=12.

Третье аналитическое выражение для границы запишем как y = f (x) и подставим в исходное уравнение:

Значение функции на концах отрезка прямой мы уже знаем. Это точка z(0,4)=16 из пункта (а) и точка z(6,0)=12 из пункта (б).

Найдём экстремальное значение функции (если оно есть) внутри этой границы:

Это точка экстремума функции внутри границы ;

z = -96/19» -5.053.

Тогда из найденных значений функций z (8/3;4/3)= -5.333 – наименьшее, а z (0;4)=16 – наибольшее.

56 Скалярные и векторные поля. Градиент , его свойства. Производная функции по направлению. Её связь с градиентом.

В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.

Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.

Рассмотрим функцию от аргументов в окрестности точки . Для любого единичного вектора определим производную функции в точке по направлению следующим образом:

Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора .

Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.

Связь с градиентом

Производную по направлению дифференцируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:

где — орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора .