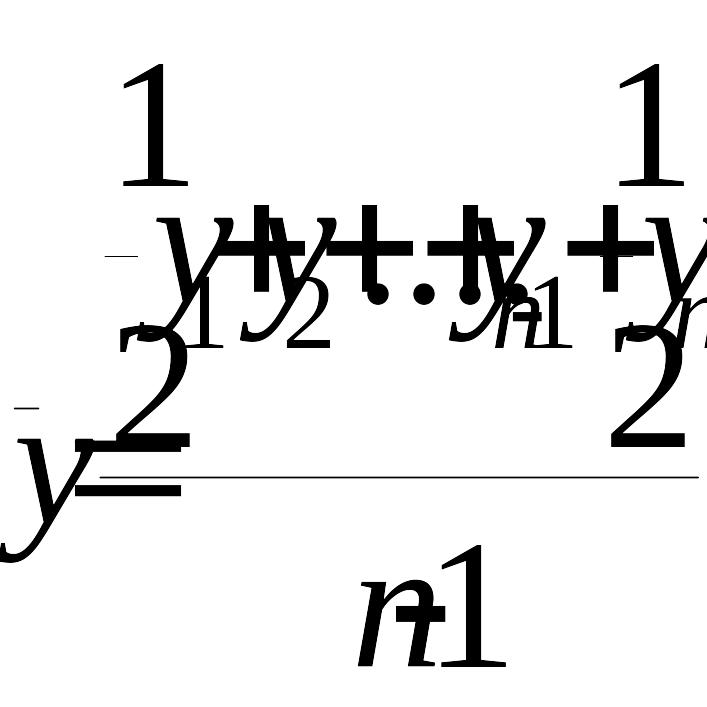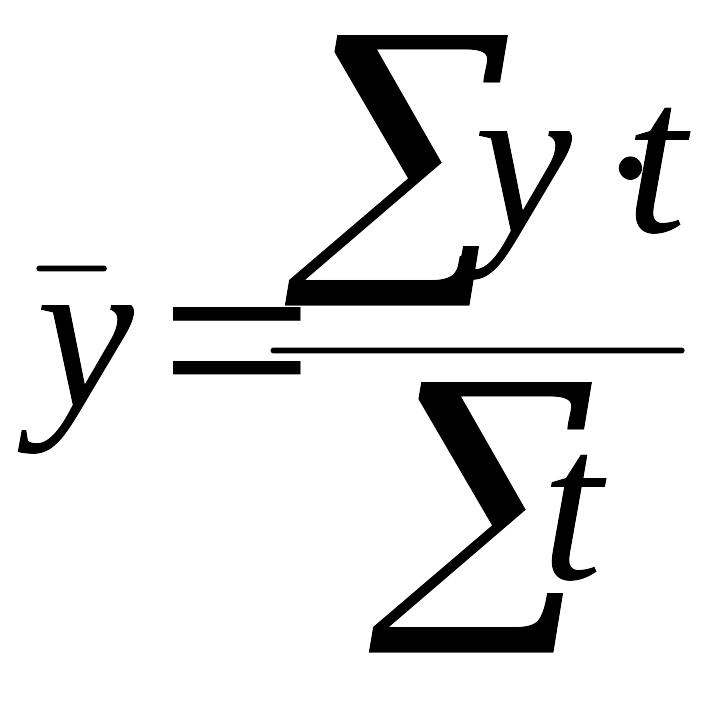13. Характеристика закономерности рядов распределения

С помощью рядов распределения решается важнейшая задача статистики – характеристика и измерение показателей колеблемости для варьирующих признаков.

В вариационных рядах существует определенная связь в изменении частот и значений варьирующего признака: с увеличением варьирующего признака величина частот вначале возрастает до определенной величины, а затем уменьшается. Такого рода изменения называются закономерностями распределения.

Важные свойства кривой распределения – это степень ее асимметрии, высоко– или низковершинность, которые в совокупности характеризуют форму или тип кривой распределения.

Важная задача – это определение формы кривой.

Характер общего распределения предполагает оценку степени его однородности и вычисление показателей асимметрии и эксцесса.

Симметричным называют распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой.

Для симметричных распределений средняя арифметическая, мода и медиана равны между собой.

Наиболее точным и распространенным является показатель, основанный на определении центрального момента третьего порядка.

Общим является нормальное распределение, которое может быть представлено графически в виде симметричной куполообразной кривой.

Куполообразная форма кривой показывает, что большинство значений концентрируется вокруг центра измерения, и в действительно симметричном одновершинном распределении средняя, мода и медиана совпадут.

Закон нормального распределения предполагает, что отклонение от среднего значения является результатом большого количества мелких отклонений, что позитивные и негативные отклонения равновероятны и что наиболее вероятным значением всех в равной мере надежных измерений является их арифметическая средняя.

Теоретической кривой распределения называют кривую распределения, которая выражает общую закономерность данного типа.

В кривой нормального распределения отражается закономерность, которая возникает при взаимодействии множества случайных причин.

Для симметричных распределений рассчитывается показатель эксцесса (островершинности).

Эксцесс – выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.

Оценка показателей асимметрии и эксцесса дает возможность сделать вывод о том, можно ли отнести данное эмпирическое распределение к типу кривых нормального распределения.

13.Понятие и виды рядов динамики. Приведение рядов динамики в сопоставимый вид

Динамическими рядами в статистической науке называют статистические данные, характеризующие изменения явлений во времени, они строятся для выявления и изучения возникающих закономерностей в развитии явлений в различных сферах жизни общества.

В рядах динамики имеются два главных элемента:

1) показатель времени (t);

2) уровни развития изучаемого явления (у).

В рядах динамики в качестве показателей времени могут выступать определенные даты времени или отдельные периоды.

Уровни, образующие ряды динамики, определяют количественную оценку развития во времени исследуемого явления или процесса, они могут выражаться относительными, абсолютными либо средними величинами. Уровни рядов динамики в зависимости от характера исследуемого явления могут относиться к определенным датам времени или к отдельным периодам.

Динамический ряд состоит из сопоставимых статистических показателей. Для правильности построения динамических рядов необходимо, чтобы состав исследуемой статистической совокупности относился к одной и той же территории, к одному и тому же кругу объектов и был рассчитан по одной и той же методологии.

Данные динамического ряда должны выражаться в одних и тех же единицах измерения, а промежутки времени между значениями ряда должны быть по возможности одинаковыми.

Ряды динамики подразделяются на моментные, интервальные и ряды средних величин.

Моментные ряды динамики отображают состояние исследуемых процессов на определенные даты времени.

Интервальные ряды динамики отображают итоги развития или функционирования исследуемых процессов за отдельные периоды времени.

Для характеристики процесса за определенный период рассчитывают средний уровень из всех членов динамического ряда.

Способы его расчета зависят от вида динамического ряда. Для интервальных рядов средняя рассчитывается по формуле средней арифметической, причем при равных интервалах применяется средняя арифметическая простая, а при неравных – средняя арифметическая взвешенная.

Для нахождения средних значений моментного ряда применяют среднюю хронологическую.

Средняя хронологическая моментного ряда равна сумме всех уровней ряда, поделенной на число членов ряда без одного, причем первый и последний члены ряда берутся в половинном размере.

Если интервалы между периодами не равны, то применяется средняя арифметическая взвешенная, а в качестве весов берутся отрезки времени между датами, к которым относятся парные средние смежных значений уровня.

14) Показатели динамики можно исчислять с переменной и постоянной базой.

Если производится сравнение каждого уровня с предыдущим уровнем, то получаются показатели динамики с переменной базой (цепные показатели динамики).

Если каждый уровень сравнивается с начальным уровнем или каким-то другим, принятым за базу сравнения, то получаются показатели динамики с постоянной базой (базисные показатели динамики).

Цепные и Базисные показатели динамики

Различают относительные величины с постоянной и переменной базой сравнения:

• Если сравнение осуществляется с одним и тем же уровнем, принятым за базу, то относительные величины динамики с постоянной базой (базисные).

• Если сравнение проводится с предшествующим уровнем, то получают относительные величины динамики с переменной базой (цепные).

Базисные — характеризуют явление за весь исследуемый период времени в целом. Начальный уровень принимается за базу, а все остальные периоды сравниваются с базой.

Цепные — характеризуют развитие явления внутри исследуемого периода времени. Каждый последующий период сравнивается с предыдущим.

15) Наиболее важна при анализе ряда динамики его основная тенденция развития, но часто по одному лишь внешнему виду ряда динамики ее установить невозможно, поэтому используют специальные методы обработки, позволяющие показать основную тенденцию ряда.

Наиболее распространёнными методами оценки тренда являются:

1. метод укрупнения интервалов;

2. сглаживание скользящей средней;

3. аналитическое выравнивание;

1. Метод укрупнения интервалов применяется для выявления тренда в рядах динамики колеблющихся уровней и заключается в преобразовании первоначального ряда динамики в ряды более продолжительных периодов. Суть метода в том, чтобы от интервалов, или периодов времени, для которых определены исходные уровни ряда динамики, перейти к более продолжительным периодам времени и посмотреть, как уровни ряда изменяются в этом случае

2. Метод скользящих средних - заключается в том, что фактические уровни ряда заменяются средними уровнями, вычисленными по определённому правилу, например:

— исходные или фактические уровни ряда динамики заменяются средними уровнями:

; ; ; …

(5.1).

В результате получается сглаженный ряд, состоящий из скользящих пятизвенных средних уровней .

Сглаживание методом скользящих средних можно производить по четырём, пяти или другому числу уровней ряда, используя соответствующие формулы для усреднения исходных уровней. Полученные при этом средние уровни называются четырёхзвенными скользящими средними, пятизвенными скользящими средними и т.д.

16) Метод аналитического выравнивания - при этом методе исходные уровни ряда динамики заменяются теоретическими или расчетными , которые представляют из себя некоторую достаточно простую математическую функцию времени, выражающую общую тенденцию развития ряда динамики (прямую, параболу, экспоненту и др.). Чаще всего в качестве такой функции выбирают прямую.

В данному случае теоретические значение можно получить исходя из уравнения прямой:

(5.2),

где - коэффициенты, определяемые в методе аналитического выравнивания;

- моменты времени, для которых были получены исходные и соответствующие теоретические уровни ряда динамики, образующие прямую, определяемую коэффициентами .

Расчет коэффициентов ведется на основе метода наименьших квадратов и рассчитываются по формулам:

(5.3); 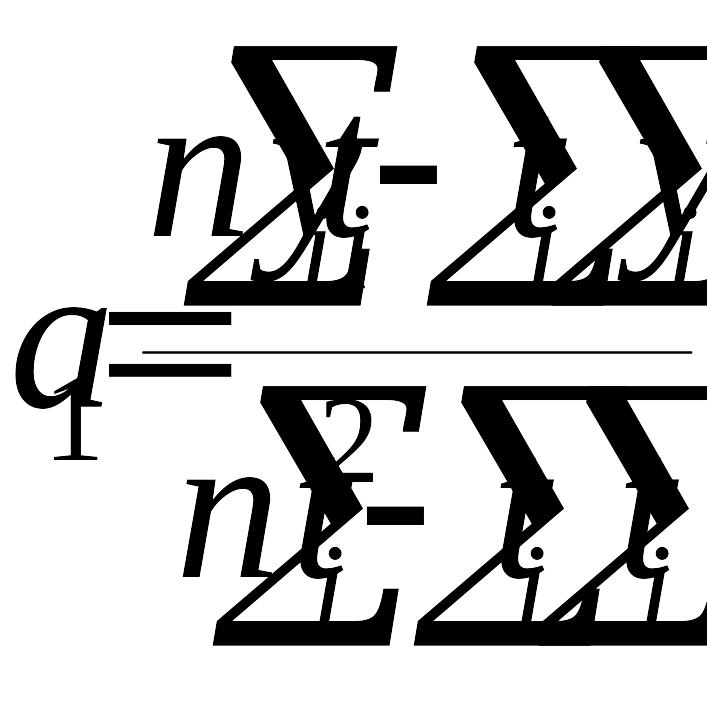(5.4);

где n — число моментов времени, для которых были получены исходные уровни ряда .

Если вместо абсолютного времени выбрать условное время таким образом, чтобы , то записанные выражения для определения упрощаются:

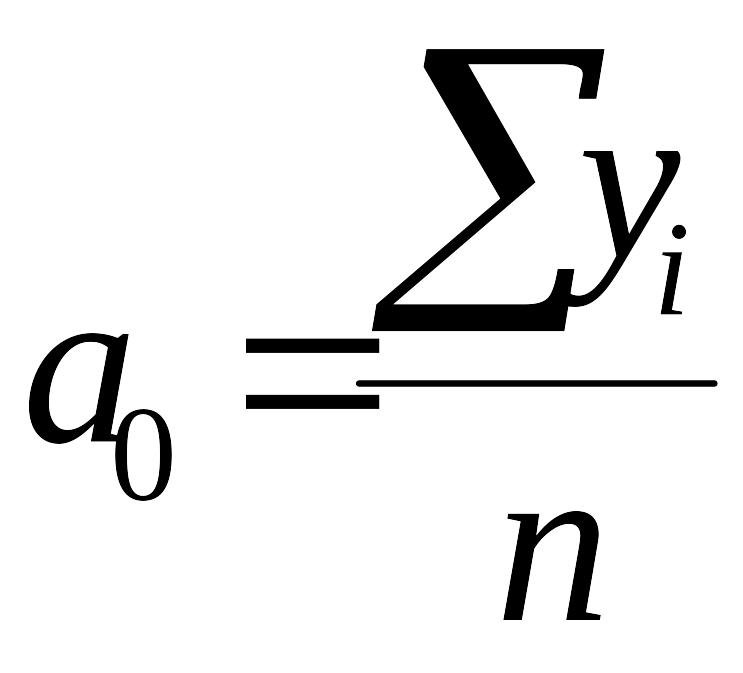(5.5);

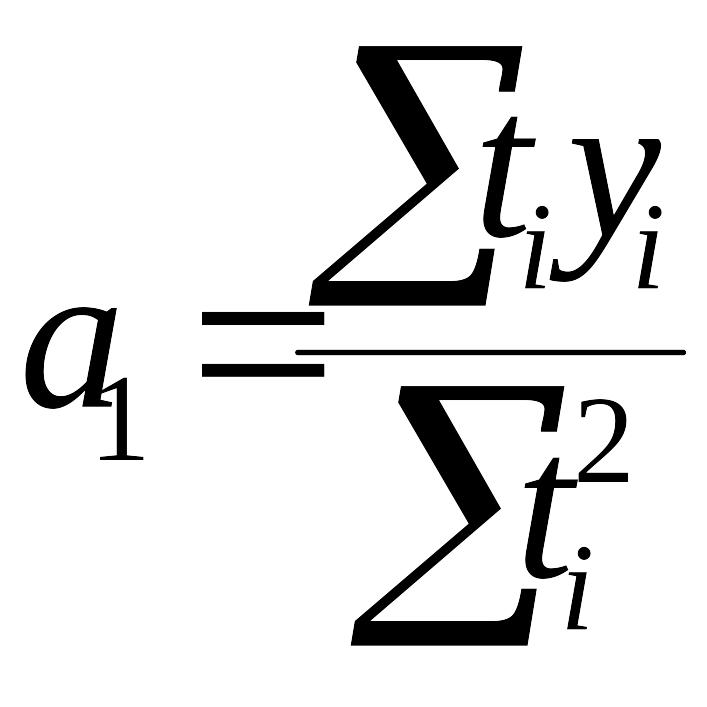
17) Методика расчета среднего уровня в рядах динамики различна, обусловлена видом ряда динамики. На примерах рассмотрим виды рядов динамики и формулы для расчета среднего уровня.Для характеристики интенсивности развития за длительный период рассчитываются средние показатели динамики, метод расчета которых представлен в таблице 5.2.

Таблица 5.2

показатель	Метод расчета
Средний уровень ряда а) для интервального ряда
б) для моментного ряда с равными интервалами
в) для моментного ряда с неравными интервалами
Средний абсолютный прирост ( )	или
Средний коэффициент роста ( )	или
Средний темп роста ( ), %
Средний темп прироста ( ), %	или
Средняя величина абсолютного значения 1% прироста ( )

18)В переводе с греческого слово «прогноз» означает предвидение, предсказание о развитии чего-либо, основанное на определенных фактических данных. В общем виде под прогнозом следует понимать научно обоснованное суждение о возможных состояниях объекта в будущем, об альтернативных путях и сроках его осуществления. Процесс разработки прогнозов называется прогнозированием. Прогнозирование есть процесс составление прогноза развития, становления, распространения чего-либо (например, науки, отрасли производства, процесса, отношений и т. д.) на основании изучения тщательно отобранных данных.

Социально-экономическое прогнозирование является одним из важнейших направлений общественного развития. Это процесс разработки прогнозов, основанный на научных методах познания социально-экономических явлений и использовании всей совокупности методов, средств и способов экономической прогностики (в перев. с греч. — методы составления, определения прогноза).

Цель прогнозирования состоит в создании научных предпосылок, включающих научный анализ тенденций развития экономики; вариантное пред¬видение предстоящего развития общественного воспроизводства, учитывающее как сложившиеся тенденции, так и намеченные цели; оценку возможных последствий принимаемых решений; обоснование направлений социально-экономического и научно-технического развития для принятия управляющих решений

Прогнозирование имеет две стороны или плоскости конкретизации: предсказательную (дескриптивную, описательную); предуказательную (предписательную). Предсказание означает описание возможных или желательных перспектив, состояний, решений проблем будущего. Предуказание означает решение этих проблем, путем использования информации о будущем в целенаправленной деятельности. Целью прогнозирования является создание научных предпосылок для принятия управленческих решений, то есть

• научный анализ тенденций развития общественного производства;

• вариантное предвиденье предстоящего развития общественного производства, учитывающее как сложившиеся, так и намеченные цели;

• оценка возможных последствий принимаемых решений, обоснование направлений социально-экономического и научно-технического развития.