
- •1.Механизм, машина. Звено, стойка. Входные и выходные звенья. Кинематические пары и их классификация. Кинематические цепи.
- •2.Число степеней свободы пространственных и плоских механизмов.
- •3.Пассивные (избыточные) связи и местные степени свободы в механизмах.
- •4.Принцип Ассура образования плоских рычажных механизмов. Структурные группы и их классификация.
- •5.Кинематический анализ плоских рычажных механизмов графическим методом.
- •6.Функции положения, аналоги скоростей и ускорений звеньев и точек.
- •7.Кинематический анализ плоских рычажных механизмов аналитическим методом.
- •8.Кинематика винтового механизма.
- •9.Виды зубчатых передач. Передаточное отношение, передаточное число.
- •11.Виды зубчатых механизмов с подвижными осями вращения. Формула Виллиса для дифференциальных и планетарных механизмов.
- •12.Классификация сил действующих в машинах.
- •13.Динамическая модель машины с одной степенью свободы. Приведение сил и масс.
- •14.Уравнения движения звена приведения в энергетической и дифференциальной формах.
- •15.Режимы движения машин. Коэффициент неравномерности движения.
- •16.Определение закона движения звена приведения при разгоне машины с электроприводом.
- •17.Определение закона движения звена приведения из уравнения движения в энергетической форме.
- •18.Определение постоянной составляющей приведенного момента инерции по заданному коэффициенту неравномерности движения.
- •20.Механическая характеристика асинхронного электродвигателя. Определение приведенного момента инерции для машин с электроприводам.
- •21.Метод кинетостатики. Определение сил инерции звеньев.
- •22.Условие статической определимости плоских кинематических цепей.
- •23.Кинетостатический силовой анализ плоских рычажных механизмов аналитическим методом.
- •25.Основные закономерности сухого трения скольжения. Трение в поступательной кинематической паре. Приведенный коэффициент трения в клиновых направлениях.
- •26.Трение скольжения во вращательной кинематической паре. Круг трения. Приведенный коэффициент трения.
- •27.Основные закономерности трения качения. Коэффициент трения качения. Условие чистого качения.
- •28.Трение в роликовых направляющих качения. Приведенный коэффициент трения.
- •29.Трение в подшипниках качения.
- •30.Механический кпд и коэффициент потерь. Кпд при последовательном и параллельном соединении механизмов.
- •31.Кпд передачи “Винт - гайка”. Явление самоторможения.
- •35.Динамическое и статическое уравновешивание вращающихся звеньев. Виды неуравновешенности, их оценка и способы устранения. Балансировка.
- •36.Уравновешивание нескольких масс, вращающихся на одном валу.
- •37.Статическое уравновешивание масс плоских рычажных механизмов (методом статического размещения масс).
- •38.Манипулятор. Переносные и ориентирующие движения. Зона обслуживания. Угол и коэффициент сервиса. Маневренность манипуляторов.
- •39.Метод преобразования координат точек и вектора в матричной форме. Составление матриц преобразования координат.
- •41.Задачи силового расчета манипулятора. Главный вектор и главный момент сил инерции звена, совершающего пространственное движение.
- •43.Основная теорема плоского сцепления (Теорема Виллиса).
- •44.Эвольвента окружности, ее уравнения и свойства.
- •45.Основные геометрические параметры зубчатых колес.
- •46.Свойства и характеристики эвольвентного зацепления цилиндрических зубчатых колес.
- •47.Качественные показатели цилиндрическик эвольвентных зубчатых передач.
- •48.Исходный производящий контур цилиндрических эвольвентных зубчатых колес. Колеса без смещения и со смещением исходного контура. Станочное зацепление.
- •49.Подрезание зубьев цилиндрических эвольвентных колес и условия его отсутствия. Коэффициент наименьшего смещения. Наименьшее число зубьев, нарезаемых без подрезания.
- •51.Особенности внутреннего зацепления цилиндрических эвольвентных зубчатых колес
- •52.Особенности косозубых цилиндрических эвольвентных колес.
- •53.Конические зубчатые передачи. Определение углов начальных конусов. Эквивалентная цилиндрическая передача.
- •55.Основные типы кулачковых механизмов. Фазы движения толкателя. Основные законы движения толкателя.
11.Виды зубчатых механизмов с подвижными осями вращения. Формула Виллиса для дифференциальных и планетарных механизмов.
Сюда относятся механизмы, в составе которых имеется хотя бы одно колесо с перемещающейся в пространстве осью вращения – сателлит.
Различают:
1) Дифференциальные механизмы.
2) Планетарные механизмы.
3) Замкнутые механизмы.
1 и 3 – центральные колеса
Н – водило
2 – сателлит
W – число степеней свободы
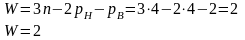
Механизм имеет два входа и один выход (или один вход и два выхода)
Получим формулу, связывающую угловые скорости звеньев в дифференциальном механизме.
Метод
обращения движения: мысленно сообщаем
всем колесам и водилу угловую скорость
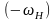 дополнительную. Тогда скорость в
обращенном движении:
дополнительную. Тогда скорость в
обращенном движении:
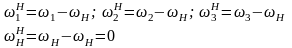
Формула Виллиса:
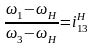
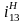 -
передаточное отношение обращенного
механизма
-
передаточное отношение обращенного
механизма
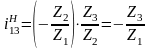
В общем виде:
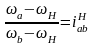
12.Классификация сил действующих в машинах.
В машинах действуют следующие основные группы сил:
1) Движущие силы – совершают положительную работу и приложены к ведущим звеньям.
2) Силы технологического (полезного) сопротивления – совершают отрицательную работу и приложены к ведомым звеньям.
3) Силы тяжести и упругости звеньев – совершают как положительную, так и отрицательную работу. За кинематический цикл их работа равна нулю.
4) Силы взаимодействия между звеньями – реакции в кинематических парах – их нормальные составляющие работы не производят (реакции идеальных связей), касательные составляющие являются силами трения и обычно относятся к вредным сопротивлениям.
5) Расчетные силы – силы инерции – для учета неравномерности.
13.Динамическая модель машины с одной степенью свободы. Приведение сил и масс.
Что бы упростить решение задач динамики, машина заменяется динамической моделью в виде вращающегося звена приведения, к которому приложен приведенный момент сил МП, и которое имеет приведенный момент инерции JП (относительно оси вращения).
МП и JП должны определяться так, чтобы в любой момент:
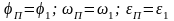 ,
где
,
где
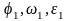 - кинематические характеристики
начального звена исполнительного
механизма. Если начальное звено совершает
поступательное движение, то динамическая
модель представляет собой точку
приведения, к которой приложена
приведенная сила FП
и которая имеет приведенную массу mП.
- кинематические характеристики
начального звена исполнительного
механизма. Если начальное звено совершает
поступательное движение, то динамическая
модель представляет собой точку
приведения, к которой приложена
приведенная сила FП
и которая имеет приведенную массу mП.
14.Уравнения движения звена приведения в энергетической и дифференциальной формах.
Согласно теореме об изменении кинетической энергии:
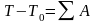 (1)
(1)
 -
кинетическая энергия машины в начальном
и конечном положениях.
-
кинетическая энергия машины в начальном
и конечном положениях.
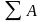 -
сумма работ всех сил на рассматриваемом
перемещении.
-
сумма работ всех сил на рассматриваемом
перемещении.
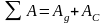 ,
где:
,
где:
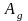 -
работа движущих сил
-
работа движущих сил
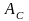 -
работа сил сопротивления
-
работа сил сопротивления
Используя приведение сил и масс, уравнение (1) можно записать следующим образом:
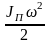 -
кинетическая энергия звена приведения
-
кинетическая энергия звена приведения
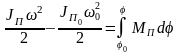 (2) – уравнение движения звена приведения
в энергетической форме.
(2) – уравнение движения звена приведения
в энергетической форме.
Согласно теореме об изменении кинетической энергии в дифференциальной форме:
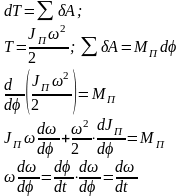
Окончательно имеем
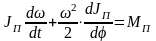 (3)
– уравнение движения приведенного
звена в дифференциальной форме.
(3)
– уравнение движения приведенного
звена в дифференциальной форме.
15.Режимы движения машин. Коэффициент неравномерности движения.
В общем случае движения машины наблюдаются в следующих стадиях:
1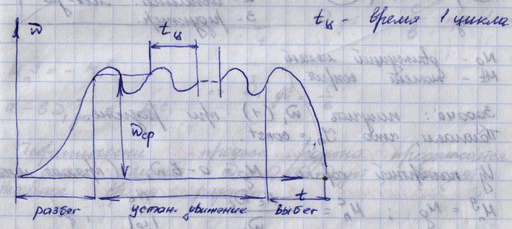 )
Разбег (разгон)
)
Разбег (разгон)
2) Установившееся движение
3) Выбег
1)
Так как
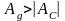 ,
то получаем:
,
то получаем:
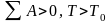 ,
ω – возрастает.
,
ω – возрастает.
2) ω – периодическая функция
Времени (в частном случае - касательная):
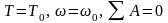 -
за цикл.
-
за цикл.
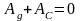 или
или
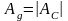
 -
коэффициент неравномерности движения
-
коэффициент неравномерности движения
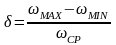
3)
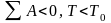 ω – убывает.
ω – убывает.
