41.Задачи силового расчета манипулятора. Главный вектор и главный момент сил инерции звена, совершающего пространственное движение.

Силовой расчет манипулятора.

Задача состоит в определении реактивных сил и моментов в кинематических парах, а также движущих сил и моментов приводных двигателей.

Главный вектор сил инерции звена:

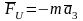
Главный момент сил инерции определяется в подвижной системе координат, связанной со звеном:

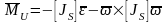
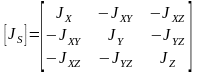- тензор инерции в центре масс.

Осевые моменты инерции:

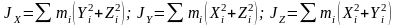
Центральные моменты инерции:

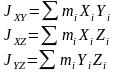
Если координатные оси совпадают с главными центральными осями инерции, то центробежные моменты инерции равны нулю. Такими осями являются оси инерции. В этом случае:

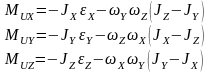
43.Основная теорема плоского сцепления (Теорема Виллиса).

Проекции звеньев высшей пары, передающей вращение между параллельными осями с заданным отношением угловых скоростей, должны быть выполнены так, что бы общая нормаль к ним в точке контакта делила межосевое расстояние на части, обратно пропорциональные угловым скоростям.

Следствия: 1) При 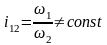полюс зацепления перемещается по межосевой линии.

2) При 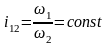полюс зацепления является неподвижной точкой и определяется радиусами 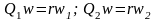, которые перемещаются одна по другой без скольжения и называются начальными.

44.Эвольвента окружности, ее уравнения и свойства.

эвольвентой окружности называется траектория общей точки прямой линии, перекатывающейся без скольжения по окружности. Эта окружность называется основной. Условие переката без скольжения - .

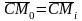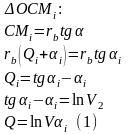
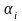- угол продолжения эвольвенты в точке “M”.

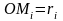- радиус – вектор в точке “M”.

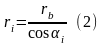
и (2) - уравнения эвольвенты в параметрической форме.

Свойства эвольвенты вытекают из условия образования:

1)Эвольвента начинается на основной окружности и делит правую и левую ветви. 2)Нормаль в эвольвенте любой ее точке касается основной окружности, а точка касания – есть центр кривизны эвольвенты.

3)Две эвольвенты одной и той же основной окружности являются эквидистсентными.

4)При эвольвента обращается в прямую линию.

45.Основные геометрические параметры зубчатых колес.

Рассмотрим торцовое сечение цилиндрического зубчатого колеса с внешними зубями.

Профиль зуба состоит из эвольвентной части и переходной кривой. Их общая точка 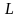- граничная точка профиля.

Окружной шар зубьев – расстояние между одноименными профилями соседних зубьев по дуге окружности. Для окружности произвольного радиуса

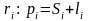
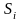- толщина зуба.

- ширина впадины.

Длину произвольной окружности можно выразить двояко:

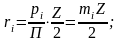
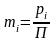- модуль зубьев на окружности.

Шаг 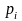и модуль зависят от того, к какой окружности они относятся.

Делительная окружность – окружность, на которой модуль зубьев стандартному модулю зуборезного инструмента.

Модуль зубьев разделительной окружности называется расчетным модулем колеса.

Радиус делительной окружности: .

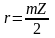На основании уравнения эвольвенты: .

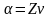- угол профиля на делительной окружности .

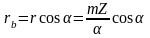
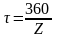- угловой шаг зубьев.

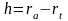- высота зуба.

- высота делительной ножки зуба.

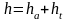
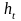- высота делительной головки зуба.

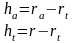
46.Свойства и характеристики эвольвентного зацепления цилиндрических зубчатых колес.

Первое свойство:

Эвольвентное зацепление обеспечивает передаточное отношение.

Линия зацепления – траектория общей точки контекста “K” профилей.

Второе свойство:

В эвольвентном зацеплении линией зацепления является прямая “n-n” – общая касательная к основным окружностям.

Угол зацепления – угол 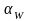между линией зацепления и перпендикуляром к межосевой линии.

Активная линия зацепления – участок линии зацепления, заключенный между окружностями вершин.

Эвольвентные профили касаются только на этом участке.

В контакте участвуют только активные профили .

Третье свойство:

При внешнем зацеплении эвольвентные профили могут касаться только в пределах отрезка 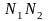, поэтому активная линия не должна выходить за предельные точки , так как там эвольвенты не имеют общей нормали и пересекаются (интерференция эвольвент).

Из 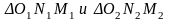связь между радиусами начальных и основных окружностей:

Межосевое расстояние:

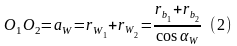
Так как радиусы 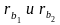являются неизменными из (1) и (2) вытекает:

Четвертое свойство:

При изменении межосевого расстояния в эвольвентном зацеплении передаточное отношение не изменяется, но изменяется угол зацепления и радиусы начальных окружностей, так что , где 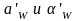- новые значения.

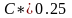Между окружностями вершин одного колеса и окружностью впадин другого должен быть радиальный зазор “C”. Обычно , где - стандартный коэффициент радиального зазора.

Тогда радиусы вершин зубьев: