1.  рационализируется подстановкой x = a sin t (или x = a cos t). Мы применяли эту подстановку в разделе 10.5. Замена переменной в неопределённом интеграле.

2. Рационализируется подстановкой (или , или ).

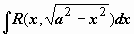3.  рационализируется подстановкой x = a tg t (или x = a ctg t, или

x = a sh t).

42.

Понятие определенного интеграла.

Пусть функция   определена и непрерывна на отрезке  ,  .  С помощью точек   разобьем отрезок   произвольным образом на  частичных отрезков   длиною  . 

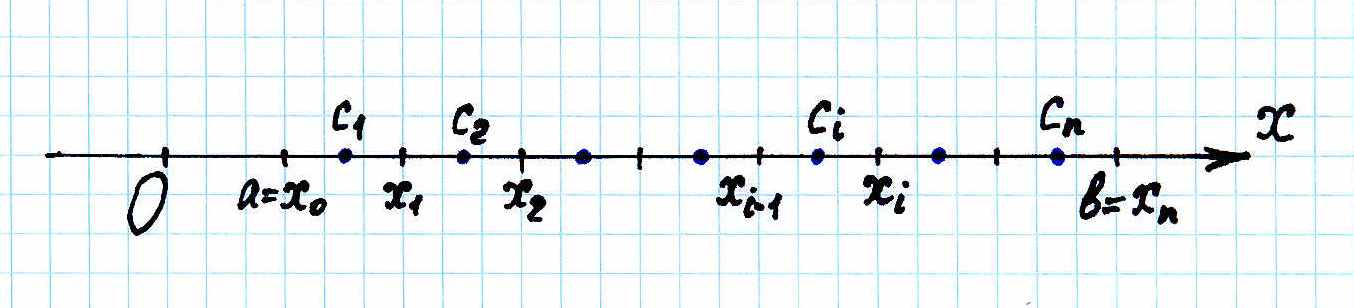
В каждом частичном отрезке   выберем произвольную точку   и вычислим значение функции в этой точке,  .  Умножим найденные значения функции   на длину соответствующего частичного отрезка   и составим сумму   всех таких произведений:

. 

43

Свойство 1. Если функция   непрерывна и интегрируема на отрезке  , то  , где   - постоянное число. То есть постоянный множитель можно выносить за знак определенного интеграла. Свойство 2. Если функции   и   интегрируемы на  , тогда интегрируема на   их сумма(разность) и    . То есть интеграл от суммы(разности) равен сумме(разности) интегралов. Свойство 3. При перестановке пределов интегрирования изменяется знак интеграла :

Свойство 4. Если функция   интегрируема на   и  , то  , то есть интеграл по всему отрезку равен сумме интегралов по частям этого отрезка. Это свойство называютаддитивностью определенного интеграла. Свойство 5. Если функция   непрерывна на отрезке   , то существует точка   такая, чт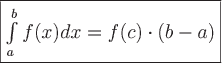о  .  Число 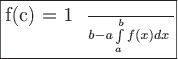  называется средним значением функции на отрезке.  Свойство 6. Если функция   сохраняет знак на отрезке   , где  , то интеграл   имеет тот же знак, что и функция. Так , если   на отрезке   , то   .  Свойство 7.Интеграл с одинаковыми пределами интегрирования равен нулю: 

44

Пусть функция f(t) определена и непрерывна на некотором промежутке, содержащем точку a. Тогда каждому числу x из этого промежутка можно поставить в соответствие число

,

определив тем самым на промежутке функцию I(x), которая называется определенным интегралом с переменным верхним пределом. Отметим, что в точке x = a эта функция равна нулю. Вычислим производную этой функции в точке x. Для этого сначала рассмотрим прира­щение функции в точке x при приращении аргумента x:

I(x) = I(x + x) – I(x) = .

Как показано на рисунке 1, величина последнего интеграла в формуле для приращения I(x) равна площади криволинейной трапеции, отмеченной штриховкой. При малых величинах x (здесь, так же как и везде в этом курсе, говоря о малых величинах приращений аргумента или функции, имеем в виду абсолютные величины приращений, так как сами приращения могут быть и положительными и отрицательными) эта площадь оказывается приблизительно равной площади прямоугольника, отмеченного на рисунке двойной штриховкой. Площадь прямоугольника определяется формулой f(x)x. Отсюда получаем соотношение

.

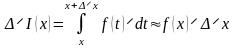В последнем приближенном равенстве точность приближения тем выше, чем меньше величина x.

Из сказанного следует формула для производной функции I(x):

.

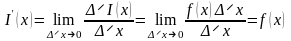Производная определенного интеграла по верхнему пределу в точке x равна значению подынтегральной функции в точке x. Отсюда следует, что функция 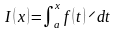является первообразной для функции f(x), причем такой первообразной, которая принимает в точке x = a значение, равное нулю. Этот факт дает возможность представить определенный интеграл в виде

. (1)

Пусть F(x) тоже является первообразной для функции f(x), тогда по теореме об общем виде всех первообразных функции I(x) = F(x) + C, где C — некоторое число. При этом правая часть формулы (1) принимает вид

I(x) – I(a) = F(x) + C – (F(a) +C) = F(x) – F(a). (2)

Из формул (1) и (2) после замены x на b следует формула для вычисления определенного интеграла от функции f(t) по промежутку [a;b]:

,

которая называется формулой Ньютона-Лейбница. Здесь F(x) — любая первообразная функции f(x).

Для того, чтобы вычислить определенный интеграл от функции f(x) по промежутку [a;b], нужно найти какую-либо первообразную F(x) функции f(x) и подсчитать разность значений первообразной в точках b и a. Разность этих значений первообразной принято обозначать символом  .

Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.

Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).

45

Если u(x), v(x) - непрерывно дифференцируемые функции, то  .  Док-во. Интегрируем равенство   в пределах от a до b:  . Функция в левом интеграле имеет первообразную uv, по формуле Ньютона-Лейбница  , следовательно,   , откуда и следует доказываемое равенство. 

Замена переменной в определённом интеграле. Теорема. Пусть функция 

1. определена, непрерывно дифференцируема и монотонна на отрезке  ,

2. ,

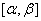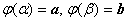3. функция   непрерывна на отрезке [a, b].

Тогда  .

• Док-во. Пусть F(x) - первообразная для функции f(x), т.е.   , тогда   - первообразная для функции  .  , что и требовалось доказать.

• 46.

• Любая точка в полярной системе координат задается полярным углом 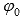  и соответствующим полярным радиусом 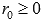 .   - это угол, отсчитываемый от полярной оси в положительном направлении (против часовой стрелки), а 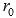  - это расстояние от заданной точки до начала координат (полюса).

• 

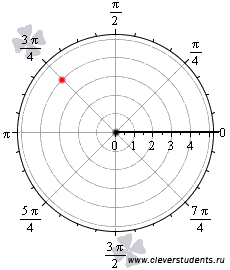
• На рисунке полюс изображен черной точкой, полярная ось – черным жирным лучом, а красная точка определяется углом 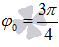  и расстоянием до полюса  . На практике очень часто полярную систему координат рассматривают вместе с прямоугольной декартовой, совмещая начала координат и полярную ось с осью абсцисс. Связь декартовых и полярных координат задается соотношениями   и обратно  .

• 

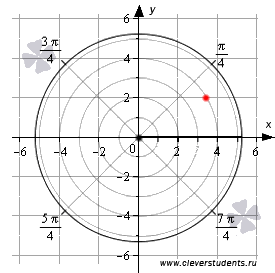
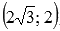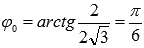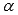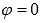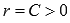• На чертеже красная точка имеет координаты  , а в полярной системе координат определяется углом   и расстоянием до полюса  . В полярной системе координат равенство   задает луч, выходящий из полюса и составляющий угол   с полярной осью (  задается в радианах или градусах). Полярная ось задается уравнением  . Равенство   задает окружность с центром в начале координат радиуса C. В свою очередь функция   определяет некоторую линию в полярных координатах. Обратите внимание, что мы будем считать функцию   всегда НЕОТРИЦАТЕЛЬНОЙ, так как с геометрической позиции она задает расстояние от полюса до точки для данного значения угла  .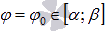 

47