Определение экстремума
Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x1< x2 выполняется неравенство (f(x1) < f (x2) (f(x1) > f(x2)).
Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f '(x) 0
(f ' (x) 0).
Точка xо называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки xо, для всех точек которой верно неравенство f(x) ≤ f(xо) (f(x) ≥ f(xо)).
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.
Точки экстремума
Необходимые условия экстремума. Если точка xо является точкой экстремума функции f(x), то либо f '(xо) = 0, либо f (xо) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.
Первое достаточное условие. Пусть xо - критическая точка. Если f ' (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
Второе
достаточное условие. Пусть
функция f(x)
имеет производную
f ' (x)
в окрестности точки xо и
вторую производную 
в
самой точке xо.
Если f ' (xо)
= 0,
>0
(
<0),
то точка xо является
точкой локального минимума (максимума)
функции f(x).
Если же
=0,
то нужно либо пользоваться первым
достаточным условием, либо привлекать
высшие производные.
На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
25.
Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке
Говорят,
что функция 
,
определенная на промежутке Х,
достигает на нем своего наибольшего
(наименьшего) значения, если существует
точка а,
принадлежащая этому промежутку, такая,
что для всех х из Х выполняется
неравенство 
.
Функция, непрерывная на отрезке, достигает на нем своего наибольшего и наименьшего значений.
Наибольшее значение М и наименьшее значение m непрерывной функции могут достигаться как внутри отрезка, так и на его концах. Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка является точкой экстремума.
Алгоритм отыскания
наибольшего и наименьшего значений
непрерывной функции
на
отрезке 
:
найти
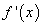;найти точки, в которых
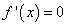или
не
существует, и отобрать из них те, что
лежат внутри отрезка
;вычислить значения функции в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции на отрезке , которые можно обозначить так:
.
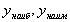Если
поставлена задача найти
для
непрерывной на 
функции
,
то она решается по тому же правилу, что
соответствующая задача для отрезка
.
Отличие: на третьем этапе вместо вычисления значений функции на концах отрезка находят пределы функции при приближении к концам интервала.
Иногда для отыскания наибольшего или наименьшего значения непрерывной функции на промежутке полезны два утверждения:
если функция имеет в промежутке Х только одну точку экстремума
,
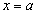причем это точка максимума, то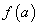 
-
наибольшее значение функции на
промежутке Х;если функция имеет в промежутке Х только одну точку экстремума , причем это точка минимума, то - наименьшее значение функции на промежуткеХ.
26.27.
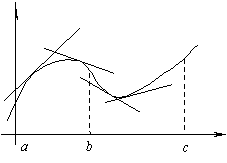
График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале. График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c). Примеры.
Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым. Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x)отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.
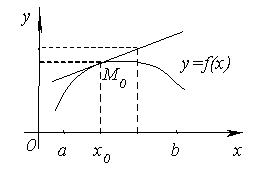
Доказательство. Предположим для определенности, что f''(x) < 0 и докажем, что график функции будет выпуклым. Возьмем
на графике функции y
= f(x) произвольную
точку M0 с
абсциссой x0 (a; b)
и проведем через точку M0 касательную.
Ее уравнение |
|
выпукла
на [–1; 1].
.
Мы должны показать, что график функции
на (a;
b) лежит
ниже этой касательной, т.е. при одном
и том же значении x ордината
кривой y
= f(x) будет
меньше ордината касательной.
Итак,
уравнение кривой имеет вид y
= f(x).
Обозначим 
ординату
касательной, соответствующую абсциссе x.
Тогда 
.
Следовательно, разность ординат кривой
и касательной при одном и том же
значении x будет 
.
Разность f(x)
– f(x0) преобразуем
по теореме Лагранжа 
,
где c между x и x0.
Таким образом,
.
К
выражению, стоящему в квадратных скобках
снова применим теорему Лагранжа: 
,
где c1 между c0 и x0.
По условию теоремы f ''(x)
< 0. Определим знак произведения второго
и третьего сомножителей.
Предположим, что x>x0. Тогда x0<c1<c<x, следовательно,
(x
– x0)
> 0 и (c
– x0)
> 0. Поэтому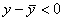 
.Пусть x<x0, следовательно, x < c < c1 < x0 и (x – x0) < 0, (c – x0) < 0. Поэтому вновь .
Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x0 (a; b), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично.
Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.
Определим достаточные условия того, что данная точка кривой является точкой перегиба.
Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x= x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба.
Доказательство. Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0.
Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
28.
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
При исследовании функции важно установить форму ее графика при неограниченном удалении точки графика от начала координат.
Особый интерес представляет случай, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.
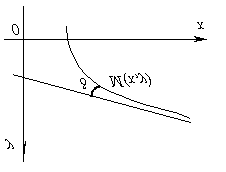
Прямая
называется асимптотой графика
функции y = f(x),
если расстояние от переменной
точки M графика
до этой прямой при удалении точки M в
бесконечность стремится к нулю, т.е.
точка графика функции при своем стремлении
в бесконечность должна неограниченно
приближаться к асимптоте.
Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.
Если обозначим через d расстояние от точки M кривой до асимптоты, то ясно, что d стремится к нулю при удалении точки M в бесконечность.
Будем в дальнейшем различать асимптоты вертикальные и наклонные.
ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ
Пусть
при x→ x0 с
какой-либо стороны функция y = f(x)неограниченно
возрастает по абсолютной величине,
т.е. 
или 
или 
.
Тогда из определения асимптоты следует,
что прямая x = x0 является
асимптотой. Очевидно и обратное, если
прямая x = x0 является
асимптотой, т. о.
.
Т
аким
образом, вертикальной асимптотой графика
функции y
= f(x) называется
прямая, если f(x) →
∞ хотя бы при одном из условий x→ x0 –
0 или x → x0 +
0, x = x0
Следовательно, для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x0, при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение x = x0.
НАКЛОННЫЕ АСИМПТОТЫ
Поскольку асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту, то ее уравнение будет y = kx + b. Наша задача найти коэффициенты k и b.
Т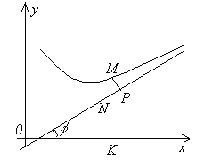
еорема.
Прямая y = kx + b служит
наклонной асимптотой при x →
+∞ для графика функции y = f(x) тогда
и только тогда, когда 
.
Аналогичное утверждение верно и при x →
–∞.
Доказательство.
Пусть MP –
длина отрезка, равного расстоянию от
точки M до
асимптоты. По условию 
.
Обозначим через φ угол наклона асимптоты
к оси Ox.
Тогда из ΔMNP следует,
что 
.
Так как φ постоянный угол (φ ≠ π/2), то 
,
но
MN = MK – NK = y - yас = f(x) - (kx+b).
Следовательно,
мы можем записать следующее равенство 
.
Так
как x →
+∞, то должно выполняться
равенство 
.
Но при постоянных k и b 
и 
.
Следовательно, 
,
т.е. 
.
Если
число k уже
известно, то 
,
поэтому 
.
Для доказательства в случае x → –∞ все рассуждения аналогичны.
Докажем
обратное утверждение. Предположим, что
существуют пределы, определяющие
числа k и b.
Тогда несложно заметить, что выполняется
равенство 
.
Действительно
Следовательно, прямая y = kx + b есть асимптота. Теорема полностью доказана.
Сделаем несколько замечаний.
Замечание 1. Теорема показывает, что для нахождения асимптот достаточно найти два указанных предела. Причем, если хотя бы один из пределов не существует или обращается в бесконечность, то кривая асимптот не имеет.
Замечание 2. В случае, когда k = 0 асимптота y = b называется горизонтальной асимптотой. Наличие горизонтальной асимптоты означает, что существуют пределы
.
Замечание 3. Пределы для отыскания k и b могут быть различны при x → +∞ и x → – ∞ и, следовательно, график функции может иметь две различные асимптоты при x → +∞ иx → –∞.
29.
Дифференцируемая функция F(x) называется первообразной функции f(x) на интервале (a, b) , если во всех точках этого интервала выполняется равенство F'(x) = f(x) .
Например, первообразной функции f(x) = x на любом интервале является функция F(x) = x2/2 , поскольку (x2/2)' = x .
Если у данной функции f(x) существует первообразная, то эта первообразная не является единственной. Так, в предыдущем примере можно взять F1(x) = x2/2 + 1 , F2(x) = x2/2 − 2 и, вообще, F(x) = x2/2 + C , где С — произвольная постоянная функция, так как
|
|
|
+ C |
|
' = x. |
|
||
|
|
|
|
|
Формула, определяющая все первообразные функции f(x), называется неопределенным интегралом функции f(x) и обозначается символом
|
|
|
При этом функция f(x) называется подынтегральной функцией, выражение f(x) dx — подынтегральным выражением, а символ ∫ — знаком интеграла. Нахождение первообразной для данной функции f(x) называется интегрированием функции f(x) .
Теорема. Если функция f(x) имеет на интервале (a, b) первообразную F(x), то
|
|
|
где C — произвольная постоянная функция.
30.
Свойства первообразных и неопределённого интеграла вытекают из определения и соответствующих свойств производных.
1. Из определения вытекает, что
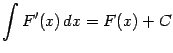
и
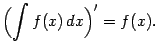
Второе равенство нужно понимать так, что производная любой из функций, составляющих неопределённый интеграл, даёт один и тот же результат, равный подынтегральной функции (это как раз и есть определение первообразной). Два написанных равенства выражают взаимную обратность операций дифференцирования и интегрирования.
2. Имеет место равенство:
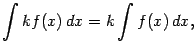
где 
--
произвольная постоянная. Для доказательства
обозначим через 
некоторую
первообразную для
,
а через 
--
некоторую первообразную для 
.
Тогда равенство означает, что 
,
где 
--
постоянная. Это равенство верно, поскольку
производные левой и правой частей дают
одно и то же: 
,
так как
--
первообразная для
,
а 
,
так как постоянный множитель можно
вынести за знак производной и 
.
Итак, постоянный множитель можно вынесить за знак интеграла.
3. Интеграл от суммы равен сумме интегралов:
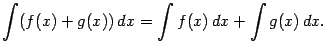
Действительно,
пусть первообразная для
равна
,
для 
равна
,
а для 
равна 
.
Тогда равенство означает, что
где 
.
Поскольку
и
то равенство верно; при этом мы воспользовались тем, что производная суммы равна сумме производных.
Свойства
2 и 3 называются свойствами линейности неопределённого
интеграла. Из них следует, что для любых
постоянных 
и 
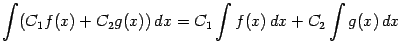
и, в частности,
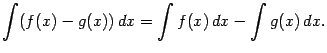
31.
Пусть
функции U(x) и V(x)═ непрерывны на некотором
промежутке X, дифферинциируемы в его
внутренних точках и═ на Х существует 
,
тогда
На
Х существует 
,
причем
=
u(x)v(x)-
,
или
;
Док-во:
d(uv)=vdu+udv; 
32
Замена переменной в неопределённом интеграле (интегрирование подстановкой).
Пусть 
.
Тогда 
.
Здесь t(x) -
дифференцируемая монотонная
функция.
Док-во непосредственно
следует из формулы для производной
сложной функции. Перепишем первый
интеграл, заменив переменную x на t: 
.
Это означает, что 
.
Заменим независимую переменную t на
функцию t = t(x): 
.
Следовательно, функция F(t(x)) является
первообразной для произведения 
,
или 
.
33
Под рациональной дробью понимается функция
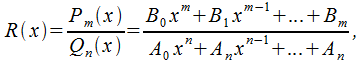
В
данном случае
-
определенные коэффициенты,
Рациональная
дробь именуется правильной, при условии,
что
,
и неправильной, в случае
.
Любую неправильную рациональную дробь можно записать в виде суммы многочлена и привильной дроби.
Допустим,
что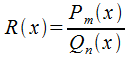
-
это неправильная рациональная дробь.
Осуществим деление числителя на
знаменатель, в итоге имеем:
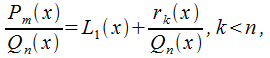
в
данном случае
и
остаток
представлены
в виде многочленов, а
-
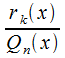это правильная рациональная дробь.