14. Дифференцирование функций заданных параметрически

  До сих пор функция записывалась в явном виде y= f(x) и в неявном F(x,y)=0. Но существует еще третий вид аналитического представления функции - это представление её в па раметрической форме в виде двух уравнений

где t - вспомогательная переменная, называемая параметром.   Заметим, что функция может быть представлена в параметрической форме различными способами.   Например, функция, записанная в неявном виде x² + y² = 1 может быть представлена в явном виде:   и в параметрической форм е:

  Заметим, что x² + y² = 1 есть уравнение окружности единичного радиуса с центром в начале координат.   В первом параметрическом представлении уравнения x² + y² = 1 параметр t изменяется от -1 до +1 и равен абциссе подвижной точки окружности, во втором случае параметр t изменяется от 0 до 2p и равен углу, образованному радиусом подвижной точки и осью Ox.   Если функция задана в явном виде y=f(x), то всегда можно записать её в неявном виде y-f(x)=0, а также в параметрической форме

От вида F(x,y)=0 не всегда возможно перейти к виду y=f(x) или x=(y), так как уравнение F(x,y)=0 может оказаться неразреш имым относительно y или x .   Лего перейти от параметрического представления функции к уравнению вида y=f(x). Для этого из первого уравнения x=x(t) нужно найтиt=t(x), если конечно это возможно , и подставить его во второе уравнение y=y(t)

y=y[t(x)]=f(x)

   От параметрического представления функции к уравнению вида F(x,y)=0 можно прийти путем исключения параметра t, если это возможно.    Уравнения y=f(x) и F(x, y)=0 служат различными аналитическими представлениями одной и той же функции F[x, f(x)]=0. Параметрические уравнения

и уравнение F(x, y)=0 представляют одну и ту же функцию, если F(x(t), y(t))=0.    Наконец, параметрические уравнения определяют ту же функцию, что и уравнение y=f(x), если

y(t)=f [ x(t) ].

   Найдем производную функции y по x в случае, когда она задана в параметрическом виде. Для этого будем рассматривать t как функцию от x. То есть t=t(x). Тогда y=y[t(x)]. Продифференцируем y как сложную функцию от x, т.е. по формуле

и применим формулу, связывающую производные обратных функций:

   Введя обозначения

,       

получим

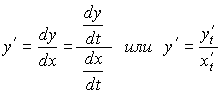
Пример.    

   Теперь найдем вторую производную от функции, заданной в параметрической форме.    Из предидущего уравнения и определения второй производной следует, что

   но

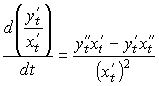
   Следовательно

   где

              

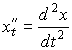
15.16

 

. Теоремы Ролля, Лагранжа и Коши.

 

Теорема Ролля.

fєC[а; b] и диф-ма на (а; b). Eсли f(а)=f(b), то Ē сє(а; b): f '(с) = 0. [рис.] y

k 

=f '(c)(x–c)+f(c)=f(c). T.o. если f удовл-ет усл-ям теоремы Роля, то на графике f есть такая точка, кас-я в которойпарал-на оси Ox. Док-во.

fєC[а;b], то по теореме Вейерштрасса найдутся такие точки c,d є[a;b]: Ā хє[а;b]f(d)≤f(x)≤f(с). 1)Если f(d)=f(с), то f- постоянная функция, => Ā хє[а;b] f '(x)=0. 2)Если f(d)<f(с), тогда хотябы одна из точек d и с не совпадает с концами отрезка [a;b]. cє(a;b) и с- точка лок-го max и по теоремеФерма f '(c)=0.

Теорема Лагранжа.

fє[а;b] и диф-ма на (а;b). Ē сє(а;b): f '(c)=(f(b)–f(a))/(b–a). [рис] (f(b)–f(a))/(b– a)=BD/AD=tgα => f '(c)=tgα. Т.о. согласно теореме Лагранжа на графике ф-ии Ē точка с, кас-я в кот-йпарал-на хорде AB. Док-во. Для док-ва расм-м F(x)=((f(b)–f(a))/(b–a))∙(x–a)–f(x). 1)Fє[a;b]. 2)F диф-ма в(a;b). 3)F(b)=((f(b)–f(a))/(b–a))(a–a)–f(a)=–f(a). F(b)=F(a). Согласно теореме Ролля Ē cє(a;b): F '(c)=0. Но F'(x)=(f(b)–f(a))/(b–a)∙1–f '(x), ((f(b)–f(a))/(b–a))–f '(c)=0.

Следствие

. fє[a;b] и f- диф-ма в (a;b). Eсли Ā xє(a;b) f '(x)=0, то f- постоянная ф-я на [a;b]. Рассм-м Āxє(a;b] и применим теорему Лагранжа на (a;x]. Ē cє(a;x): (f(x)–f(a))/(x–a)=f '(c)=0 => Ā xє(a;b] f(x)=f(a) =>Ā xє[a;b] f(x)=f(a).

Теорема Коши.

Пусть ф-ии f и gєC[а; b] и диф-мы на (а;b), причем Ā хє(а;b): g'(х)≠0. Тогда Ē сє(а;b):(f(b)–f(a))/(g(b)–g(a))=f '(c)/g'(c). Док-во. Отметим, что в левой части рав-ва знам-ль не обращ-ся в 0, т.к.если доп-ть, что g(b)=g(a), то по теореме Ролля Ē cє(a;b): g'(c)=0 => получим противоречие. Рассм-мF(x)=f(x)–(f(b)–f(a))/(g(b)–g(a))∙(g(x)–g(a)). 1)F- непр-на, т.е. FєC[a;b]. 2)F диф-ма в (a;b). 3)F(a)=f(a),F(b)=f(b)–(f(b)–f(a))/(g(b)–g(a)) ∙ (g(b)–g(a))=f(a). Т.о. F удовл-ет усл-ям теоремы Ролля, поэтому Ē cє(a;b):F '(c)=0. Но F '(x)=f '(x)–(f(b)–f(a))/(g(b)–g(a))∙g'(x). Подставляя сюда число с получим искомое рав-во.

Замечание

. Теорема Коши явл-ся обощением теоремы Лагранжа (f(b)–f(a))/(g(b)–g(a))=f '(c)/g'(c).

17.

 Дифференцирование функций, заданных неявно

Пусть значения переменных х и у связаны уравнением

F(x, y) = 0.                                                                                                        (1)

Если функция y = f(x), определенная на некотором интервале (а,в), такая, что уравнение (1) при подстановке в него вместо у выражения f(x) обращается в тождество, то говорят, что уравнение (1) задает функцию y = f(x) неявно или что функция y = f(x) есть неявная функция.

Укажем правило нахождения производной неявной функции, не преобразовывая ее в явную, то есть не представляя в виде y = f(x), так как часто это преобразование бывает технически сложным или невозможным.

Для нахождения производной у'_х неявной функции, нужно продифференцировать по х обе части равенства (1), учитывая, что у есть функция от х. Затем из полученного равенства выразитьу'_х.

18.

Теорема 17. (Правило Лопиталя раскрытия неопределенностей вида  ).

Пусть функции y = f(x), y = g(x) непрерывны и дифференцируемы в некоторой окрестности числа a (a может равняться ∞), за исключением, быть может, числа a ; при этом g, g' не равны нулю в этой окрестности.

Кроме этого, пусть  .

Тогда, если