
Билет №7
1.)
Построение начального
опорного решения и переход от одного
опорного решения к другому в симплексном
методе (вывод формул). Получим
правило выбора разрешающих элементов
для преобразований Жордана, обеспечивающее
сохранение неотрицательности правых
частей системы уравнений. Пусть
разрешающим элементом для преобразования
Жордана является коэффициент
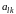 при неизвестной
при неизвестной
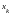 в уравнении с номером l.
В результате преобразования Жордана
правые части уравнений, как известно,
пересчитываются по следующим формулам:
в уравнении с номером l.
В результате преобразования Жордана
правые части уравнений, как известно,
пересчитываются по следующим формулам:
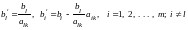 .
1. Чтобы правая часть
.
1. Чтобы правая часть
 уравнения с разрешающим элементом
оставалась неотрицательной, надо:
уравнения с разрешающим элементом
оставалась неотрицательной, надо:
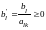 .
Так как
.
Так как
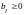 ,
то первое условие для
состоит в том, что
,
то первое условие для
состоит в том, что
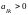 .
.
2. Неотрицательные правые части остальных
уравнений,
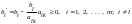 .
Для получения требований, налагаемых
на
.
Для получения требований, налагаемых
на
 ,
рассмотрим два случая: а) если
,
рассмотрим два случая: а) если
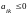 ,
то из-за
,
то из-за
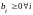 ,
,
,
без дополнительных условий имеем
,
,
,
без дополнительных условий имеем
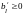 ;
;
б) если же
 ,
то неравенство
,
то неравенство
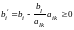 ,
,
 .
Данное неравенство должно выполняться
для любого уравнения с номером i,
в котором
.
Для удобства вычислений: вспомогательный
параметр
.
Данное неравенство должно выполняться
для любого уравнения с номером i,
в котором
.
Для удобства вычислений: вспомогательный
параметр
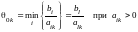 ,
k
номер вектора условия
,
k
номер вектора условия
 ,
вводимого в базис, l
номер вектора
,
вводимого в базис, l
номер вектора
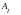 ,
выводимого из базиса.
,
выводимого из базиса.
С помощью данного условия возможно выбрать разрешающий элемент в любом столбце k матрицы системы ограничений, в котором имеется хотя бы один положительный элемент. При нарушении данного условия выбора разрешающего элемента в правой части системы уравнений появляются отрицательные величины. Используя данное условие, можно найти начальное опорное решение.
Аналогичное условие может быть использовано при переходе от одного опорного решения к другому. Пусть система уравнений-ограничений с помощью подходящего выбора разрешающих элементов приведена к равносильной разрешённой так, что правые части системы сохранились неотрицательными, и имеет вид

 .
.
Тогда базисное решение
 является допустимым и опорным решением
с базисом из единичных векторов
является допустимым и опорным решением
с базисом из единичных векторов
 .
.
Очевидно,
для перехода от этого опорного решения
к новому необходимо использовать
соотношение
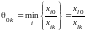 при
при
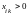 ,
где k
номер вектора, вводимого в базис, l
номер вектора,
выводимого из базиса,
,
где k
номер вектора, вводимого в базис, l
номер вектора,
выводимого из базиса,
 координаты опорного
решения,
координаты опорного
решения,
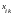 коэффициенты
разложения вектора
коэффициенты
разложения вектора
 по базису опорного решения.
по базису опорного решения.
2.) Теорема о двух линейно независимых системах векторов. Теорема о числе векторов, входящих в базис. Ранг системы векторов. Т. Если система линейно независимых векторов, содержащая n векторов, разлагается по другой линейно независимой системе векторов, содержащей m векторов, то n≤m. Док-во. Пусть есть линейно независимые системы векторов А1,А2, …, Аn и В1,В2,…,Вm, и векторы первой системы разлагаются по векторам второй системы. Предположим, что n>m.
 . Существует
ƛ1, ƛ2,…, ƛn,
при котором А1 ƛ1+А2
ƛ2+…+ Anƛn.
Равняется нулевому вектору Θ.
. Существует
ƛ1, ƛ2,…, ƛn,
при котором А1 ƛ1+А2
ƛ2+…+ Anƛn.
Равняется нулевому вектору Θ.
 .
Должна иметь ненулевое решение. Эта
система имеет ненулевое решение ƛ1,
ƛ2,…, ƛn, так
как по предположению число неизвестных
n больше числа m.
Это противоречит тому, что система
векторов А1,А2, …, Аn
является линейно зависимой.
Предположение n>m
неверно. Следовательно, n≤m.
Т о числе векторов, входящих в базис.
Любой базис системы векторов содержит
одно и то же число векторов. Число
векторов, входящих в базис системы
векторов, называется рангом системы
векторов. Док-во. Пусть система векторов
А1,А2, …, Аn
имеет два базиса. Базис Б1=(
В1,В2,…,Вm)
содержит m векторов, а
базис Б2=(C1,
C2,...,Ck)
содержит k векторов. Каждый
из базисов представляет собой независимую
систему векторов и векторы каждого
базиса разлагаются по векторам другого
базиса. Поэтому по теореме о линейно
независимых векторах m≤k
и k≤m.
.
Должна иметь ненулевое решение. Эта
система имеет ненулевое решение ƛ1,
ƛ2,…, ƛn, так
как по предположению число неизвестных
n больше числа m.
Это противоречит тому, что система
векторов А1,А2, …, Аn
является линейно зависимой.
Предположение n>m
неверно. Следовательно, n≤m.
Т о числе векторов, входящих в базис.
Любой базис системы векторов содержит
одно и то же число векторов. Число
векторов, входящих в базис системы
векторов, называется рангом системы
векторов. Док-во. Пусть система векторов
А1,А2, …, Аn
имеет два базиса. Базис Б1=(
В1,В2,…,Вm)
содержит m векторов, а
базис Б2=(C1,
C2,...,Ck)
содержит k векторов. Каждый
из базисов представляет собой независимую
систему векторов и векторы каждого
базиса разлагаются по векторам другого
базиса. Поэтому по теореме о линейно
независимых векторах m≤k
и k≤m.
Билет №8
