Билет№1

1.) Основой для решения экономических задач являются мат. Модели. Мат модель – совокупность мат. соотношений, описывающих суть задачи. Общая задача мат. Программирования формируется след. Образом: найти переменные Х=(х1, х2,….хn), обеспечивающие экстремум целевой функции задачи: Z(X)=F(x1,x2,…xn)->max(min)

И удовлетворяющие систему ограничений

Фi(x1,x2,…,xn)=0,i=1,2,….l,

Фi(x1,x2,…..xn) ≤0, i=l+1,l+2,….,m.

Задача мат. Программирования называется задачей линейного программирования, если все функции, входящие в мат. модель линейные.

В общем случае задача линейного програм. Мб записана в таком виде:

Z(x)= c1x1+c2x2+…+cnxn->max(min),

a11x1+f12x2+…a1nxn=b1

………………………………..

al1x1+al2x2+…+alnxn=bl,

a(l+1)x1+a(l+1)2x2+…+a(l+1)nxn≤bl+1,

……………….

amlx1+am2x2+…+amnxm≤bm,

данная запись означает следующее: найти экстремум целевой функции и соответ. Ему переменные при условии, что эти переменные удовлетворяют системе ограничений и условиям неотрицательности.

задача исп-я ресурсов;

b – запасы ресурсов, aij – расход каждого i-ого вида ресурса на изготовление единицы j-ой продукции, сj – прибыль

Z(x)=c1x1+c2x2+…+cnxn → max

a11x1+a12x2+…+a1nxn≤b1

a21x1+a22x2+…+a2nxn≤b2

………………………………

am1x1+am2x2+…+amnxn≤bm

xi ≥ 0

2) задача о составлении рациона питания;

b- животные должны получать ежедневно не менее b, aij – содержание iогопит вещества в единице jого вида корма, cj – стоимость единицы jого вида корма.

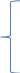Z(x)=c1x1+c2x2+…+cnxn → min

a11x1+a12x2+…+a1nxn≥b1

a21x1+a22x2+…+a2nxn≥b2

………………………………

am1x1+am2x2+…+amnxn≥bm

xi ≥ 0

2.) Общая теория систем уравнений. Теорема Кронекера-Капелли.

Пусть имеется система линейных уравнений:

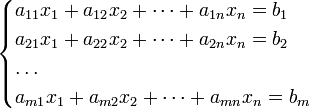. Ее можно записать а векторном виде:

A₁x₁+A₂x₂+…+A_jx_j+…+A_nx_n=B, где A_j= , (J=1, 2 … n). B = . Однородная сис-ма ур-ний, соответствующая данной сис-ме, имеет вид: A₁x₁+A₂x₂+…+A_jx_j+…+A_nx_n=0. В матричной записи эти сис-мы имеют вид: AX=B и AX=0. Матрица A называется матрицей системы уравнений.

A= =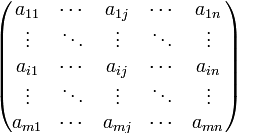

Матрица 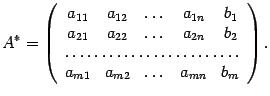называется расширенной матрицей системы уравнений. Рангом матрицы называют ранг системы векторов-столбцов матрицы. Ранг матрицы системы обозначают r(A)=r(A_1, A₂, …, A_n).

Т (Кронекера-Капелли). Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы r( ) равнялся рангу матрицы системы r(A), т. е. r( ) = r(A).

Данное условие считается более удобным, чем способ определения совместности системы, используемый в методе ЖорданаГаусса. Док:Необходимость. Система уравнений

совместна. Покажем, что r( ) = r(A).

Пусть система имеет некоторое частное решение К = ( ), т. е.

. Это равенство можно рассматривать как

разложение вектора В по векторам . Пусть r(A) = r и векторы образуют базис системы . Тогда любой из векторов

(j = 1, 2, …, n) разлагается по этому базису. Вектор B разлагается по векторам . Следовательно, он разлагается и по векторам . Любая максимальная линейно независимая подсистема векторов является базисом системы векторов. В системе подсистема является максимальной линейно независимой подсистемой, так как B разлагается по ней. Следовательно, r( ) = r(A).

Достаточность. Пусть r(A) = r( ) = r. Докажем, что в этом случае система уравнений совместна. Пусть базис системы векторов образуют векторы . Так как r( ) =r, то любая подсистема, состоящая из rлинейно независимых векторов является ее базисом (см. теорему 3.6). Такой подсистемой для системы является . Следовательно, вектор В разлагается по векторам , .

Это соотношение можно дополнить равными нулю слагаемыми, не нарушая равенства, и записать в виде .Данное соотношение является подтверждением того, что система уравнений имеет решение К = ( ), т. е. она совместна.