
- •1 Вопрос: определение производной
- •Правило Лопиталя
- •11 Вопрос: дифференциал функции Понятие дифференциала функции
- •16 Вопрос: интегрирование тригонометрических функций 17 вопрос: интегрирование рациональных дробей
- •18 Вопрос: определенный интеграл, геометр. Смысл
- •19 Вопрос: интегрирование по частям, замена переменной в определенном интеграле
- •1Интегрирование по частям
- •21 Вопрос: определенный интеграл от четных и нечетных фун-ции по симметричному промежутку
- •22 Вопрос: не собственный интеграл
- •23 Вопрос: фун-ции нескольких переменных, частные производные
- •24 Вопрос: дифференциал фун-ции 2 переменных
- •25 Вопрос: частные производные 2 порядка
- •26 Вопрос: ряды, свойство рядов
- •1.1Сходящихся числовых рядов.
- •27 Вопрос: признаки сходимости и признаки сравнения рядов
- •1.2.1Первый, второй и третий признаки сравнения.
- •1.2.2Признак Даламбера.
- •28 Вопрос: обобщенный гармонически ряд
- •29 Вопрос: знакочередующийся ряды
- •1.3[Править]Признак Лейбница
1 Вопрос: определение производной
Рассмотрим
функцию
y=f(x),
дадим
аргументы
х
приращение
в
дельту
х,
тогда
функция
получит
приращение
?y=f(x
+ ?x)-f(x)
 Пусть
существует
придел
, который
называется
производной
функцией
y
в
точки
x,
и
обозначается
. Другие
обозначения
придела(производной):
производная
по
времени
обозначается
точкой:
Определение
производной:
Производной
функции
y=f(x)
в
точки
x,
называется
придел
отношения
приращения
функции
в
этой
точке,
приращение
аргумента
при
условии
приращение
аргумента
стремится
к
0, если
что
этот
придел
существует.
Формула:
Функция
имеющая
производную
в
данной
точке
называется
дифференцируемой
в
этой
точке.
Пусть
существует
придел
, который
называется
производной
функцией
y
в
точки
x,
и
обозначается
. Другие
обозначения
придела(производной):
производная
по
времени
обозначается
точкой:
Определение
производной:
Производной
функции
y=f(x)
в
точки
x,
называется
придел
отношения
приращения
функции
в
этой
точке,
приращение
аргумента
при
условии
приращение
аргумента
стремится
к
0, если
что
этот
придел
существует.
Формула:
Функция
имеющая
производную
в
данной
точке
называется
дифференцируемой
в
этой
точке.
2
вопрос:
Геометрический
смысл
производной
Рассмотрим
график
функции
y=f(x)
и
прямую
пересекающую
этот
график
в
точках
М
и
М(
такая
прямая
называется
секущей) Касательная
к
кривой
в
точке
М,
называется
придельное
положение
секущей
ММ’,
при
условии,
что
точки
М’,
не
ограничена
приближается
по
кривой
в
точке
М.
Касательная
к
кривой
в
точке
М,
называется
придельное
положение
секущей
ММ’,
при
условии,
что
точки
М’,
не
ограничена
приближается
по
кривой
в
точке
М.
 k’=tg
(MM’),
M’?M(устремим),
угол
угол
между
y,
угол
?(альфа)
угол
касательной
в
точке
k’=tg
(MM’),
M’?M(устремим),
угол
угол
между
y,
угол
?(альфа)
угол
касательной
в
точке
Ю, ?x?0, ??, tg ? tg?. Таким образом коэффициент касательной = tg?=приделу , Таким образом угловой коэффициент касательной к графику функции y=f(x), равен значению ее производной в точке касания. Уравнение касательной к графику f(x) обозначем ее точкой
3
вопрос:
связь
между
непрерывностью
и
дифферинцированностью
функции.
Дифференциал:
, Непрерывная
функция:
Теорема:
Если
функция
дифференцирована
в
некоторой
точке,
то
она
в
этой
точке
непрерывна,
из
существующей
производной
следует
непрерывность
функции(обратная
не
верна,
непрерывная
функция
может
не
быть
дифференцирована)
Покажем,
что
функция
может
быть
непрерывна,
но
при
этом
не
иметь
производной.
 y=,
x=0
Эта
функция
не
является
дифференциалом.
y=,
x=0
Эта
функция
не
является
дифференциалом.
4
вопрос:
правила
дифференцирования(таб.
Производных)
Если с -
постоянное
число,
и
u = u(x), v = v(x) - некоторые
дифференцируемые
функции,
то
справедливы
следующие
правила
дифференцирования:
1)
(с)
' = 0, (cu) ' = cu';- производная
постоянной
величины
постоянно
равна
0
2) (u+v)' = u'+v'; - производная
суммы(разности
функции)=
сумме(разности
производных).
Доказательство
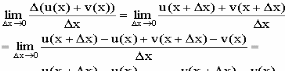 3)
(uv)'
= u'v+v'u; - производная
произведения.
Доказательство:
3)
(uv)'
= u'v+v'u; - производная
произведения.
Доказательство:
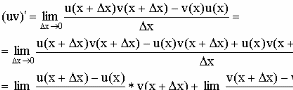 4)(C*U')=C*U'
(C'*U(=0)+C*U') – постоянный
множитель,
выносится
за
знак
производной
5)
(u/v)' = (u'v-v'u)/v2;
-
производного
частого.
Доказательство:
4)(C*U')=C*U'
(C'*U(=0)+C*U') – постоянный
множитель,
выносится
за
знак
производной
5)
(u/v)' = (u'v-v'u)/v2;
-
производного
частого.
Доказательство:
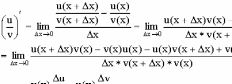 Таблица
производных:
1)
1=
2) (sinx)’=cosx
3) (cosx)’=
-sinx
4)(tgx)’=
5) (ctgx)’=
-
6)()’=*lna
6’) (ex)’=ex
7) (logax)’=
7’)(lnx)=
8)(arcsinx)’=
9) (arccosx)’=
-
10)(arctgx)’=
11) (arcctgx)’=
-
Примеры:
Таблица
производных:
1)
1=
2) (sinx)’=cosx
3) (cosx)’=
-sinx
4)(tgx)’=
5) (ctgx)’=
-
6)()’=*lna
6’) (ex)’=ex
7) (logax)’=
7’)(lnx)=
8)(arcsinx)’=
9) (arccosx)’=
-
10)(arctgx)’=
11) (arcctgx)’=
-
Примеры:
5 вопрос: производная сложной функции и обратной функции Сложная функция называется функция аргумент которой в свою очередь является функцией(т.е. функция от функции). y=f(f(x)) y=f(z), z=f(x)- промежуточный аргумент. Х- независимая переменная. Теорема: если у=f(z) и z=f(x) дифференцируемые функции от своих аргументов, то производная сложной функции y=f((x)) равна произведению производной функции f по промежуточному аргументу z на производную функцию z по независимой переменной x. y’=f’((x))=f’(z)*(x) Примеры:
Теорема. Если
для
функции y=f(x) существует
обратная
функция x=g(y),
которая
в
некоторой
точке у0 имеет
производную g '(v0),
отличную
от
нуля,
то
в
соответствующей
точке x0=g(x0)
функция y=f(x) имеет
производную f '(x0),
равную ![]() ,
т.е.
справедлива
формула
,
т.е.
справедлива
формула![]() .
.
Доказательство. Т.к. x=g(y) дифференцируема в точке y0, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точкеx0=g(y0). Следовательно, при Δx?0 Δy?0.
Покажем,
что ![]() .
.
Пусть ![]() .
Тогда
по
свойству
предела
.
Тогда
по
свойству
предела ![]() .
Перейдем
в
этом
равенстве
к
пределу
при
Δy?0.
Тогда
Δx?0
и
α(Δx)?0,
т.е.
.
Перейдем
в
этом
равенстве
к
пределу
при
Δy?0.
Тогда
Δx?0
и
α(Δx)?0,
т.е. ![]() .
.
Следовательно,
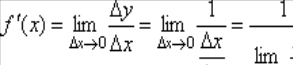 ,
,
что и требовалось доказать.
Эту
формулу
можно
записать
в
виде ![]() .
.
Рассмотрим применение этой теоремы на примерах.
Примеры.
1)y =
ex.
Обратной
для
этой
функции
является
функция x=
ln y.
Мы
уже
доказали,
что ![]() .
Поэтому
согласно
сформулированной
выше
теореме
.
Поэтому
согласно
сформулированной
выше
теореме
![]()
Итак,
(ex)
' = ex2)Аналогично
можно
показать,
что
(ax)
' = ax·lna..
3)y =
arcsin x.
Рассмотрим
обратную
функцию x =
sin y.
Эта
функция
в
интервале
– π/2<y<π/2
монотонна.
Ее
производная x '
= cos yне
обращается
в
этом
интервале
в
нуль.
Следовательно,
по
теореме
о
производной
обратной
функции
![]() .
.
Но
на
(–π/2;
π/2) ![]() .
.
Поэтому
![]()
4)y =
arctg x.
Эта
функция
по
определению
удовлетворяет
условию
существования
обратной
функции
на
интервале
–π/2< y <
π/2.
При
этом
обратная
функция x =
tg y монотонна.
По
ранее
доказанному
![]() .
Следовательно, y '
= cos2 y .
Но
.
Следовательно, y '
= cos2 y .
Но ![]() .
.
Поэтому
![]()
Используя эти формулы, найти производные следующих функций:

6
вопрос:
производная
функция
заданной
параметрически,
производные
высших
порядков
Пусть
задана
зависимость
двух
переменных ![]() и
и ![]() от
параметра
от
параметра ![]() ,
изменяющегося
в
пределах
от
,
изменяющегося
в
пределах
от ![]() до
до ![]() :
:
![]()
Пусть
функция ![]() имеет
обратную:
имеет
обратную: ![]() .
Тогда
мы
можем,
взяв
композицию
функций
.
Тогда
мы
можем,
взяв
композицию
функций ![]() и
и ![]() ,
получить
зависимость
от
:
,
получить
зависимость
от
: ![]() .
Зависимость
величины
от
величины
,
заданная
через
зависимость
каждой
из
них
от
параметра
в
виде
.
Зависимость
величины
от
величины
,
заданная
через
зависимость
каждой
из
них
от
параметра
в
виде ![]() ,
называется функцией
,
называется функцией ![]() ,
заданной
параметрически.
,
заданной
параметрически.
Производную
функции ![]() ,
заданной
параметрически,
можно
выразить
через
производные
функций
,
заданной
параметрически,
можно
выразить
через
производные
функций ![]() и
и ![]() :
поскольку
и,
по
формуле
производной
обратной
функции,
:
поскольку
и,
по
формуле
производной
обратной
функции, 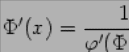 ,
то
,
то
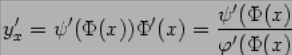
где - значение параметра, при котором получается интересующее нас при вычислении производной значение .
Заметим,
что
применение
формулы
приводит
нас
к
зависимости
между ![]() и
,
снова
выраженной
в
виде
параметрической
зависимости:
и
,
снова
выраженной
в
виде
параметрической
зависимости: ![]() ,
, ![]() ;
второе
из
этих
соотношений --
то
же,
что
участвовало
в
параметрическом
задании
функции
.
Несмотря
на
то,
что
производная
не
выражена
через
в
явном
виде,
это
не
мешает
решать
нам
задачи,
связанные
с
нахождением
производной,
найдя
соответствующее
значение
параметра
.
Покажем
это
на
следующем
примере.
;
второе
из
этих
соотношений --
то
же,
что
участвовало
в
параметрическом
задании
функции
.
Несмотря
на
то,
что
производная
не
выражена
через
в
явном
виде,
это
не
мешает
решать
нам
задачи,
связанные
с
нахождением
производной,
найдя
соответствующее
значение
параметра
.
Покажем
это
на
следующем
примере.
Пример 4.22 Пусть зависимость между и задана параметрически следующими формулами:
![]()
Найдём
уравнение
касательной
к
графику
зависимости
в
точке ![]() .
.
Значения ![]() и
и ![]() получаются,
если
взять
получаются,
если
взять ![]() .
Найдём
производные
и
по
параметру
:
.
Найдём
производные
и
по
параметру
:
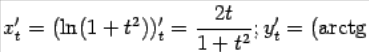
Поэтому
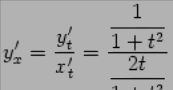
При получаем значение производной
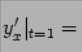
это
значение
задаёт
угловой
коэффициент ![]() искомой
касательной.
Координаты
искомой
касательной.
Координаты ![]() и
и ![]() точки
касания
заданы
в
условии
задачи.
Значит,
уравнение
касательной
таково:
точки
касания
заданы
в
условии
задачи.
Значит,
уравнение
касательной
таково:

Заметим, что исходя из полученной параметрической зависимости , , мы можем отыскать вторую производную функции по переменной :
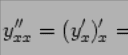
Пример 4.23 Пусть дана та же зависимость между и , что в предыдущем примере:
Найдём
выражение
для
второй
производной ![]() через
параметр
.
Ранее
мы
получили,
что
через
параметр
.
Ранее
мы
получили,
что 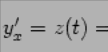 .
Поэтому
.
Поэтому 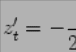 ;
производную
;
производную  мы
нашли
выше.
Получаем:
мы
нашли
выше.
Получаем:
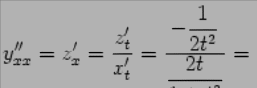
Можно
получить
и
явный
вид
производной
второго
порядка
от
параметрически
заданной
функции,
если
подставить 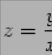 в
формулу
в
формулу 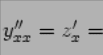 ;
при
этом
получим:
;
при
этом
получим:
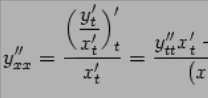 Пусть
функция
y=f(x) дифференцируема
на
некотором
отрезке
[a; b]. Значение
производной
f'(x), вообще
говоря,
зависит
от
x, т.е.
производная
f'(x) представляет
собой
тоже
функцию
переменной
x. Пусть
эта
функция
также
имеет
производную.
Дифференцируя
ее,
получим
так
называемую
вторую
производную
от
функции
f(x).
Пусть
функция
y=f(x) дифференцируема
на
некотором
отрезке
[a; b]. Значение
производной
f'(x), вообще
говоря,
зависит
от
x, т.е.
производная
f'(x) представляет
собой
тоже
функцию
переменной
x. Пусть
эта
функция
также
имеет
производную.
Дифференцируя
ее,
получим
так
называемую
вторую
производную
от
функции
f(x).
Производная от первой производной называется производной второго порядка или второй производной от данной функции y=f(x) и обозначается y''или f''(x). Итак, y'' = (y')'.
Например, если
у = х5, то y'= 5x4, а y''= 20x4.
Аналогично, в свою очередь, производную второго порядка тоже можно дифференцировать. Производная от второй производной называется производной третьего порядка или третьей производной и обозначается y'''или f'''(x).
Вообще, производной n-го порядка от функции f(x) называется производная (первая) от производной (n - 1)-го порядка и обозначается символом y(n) или f(n)(x): y(n) = (y(n-1))'.
Таким образом, для нахождения производной высшего порядка от данной функции последовательно находят все ее производные низших порядков.
Примеры.
1. Найти производную четвертого порядка функции y= ln x.
.2. Найти производную n-го порядка функции y = ekx.
y'= k·ekx, y''= k2·ekx, y''' = k3·ekx, …,y(n) =kn·ekx.
7 вопрос: возрастание и убывание функции, точки экстремы Возрастание и убывание функции, функция y = f (x) называется возрастающей на отрезке [a, b], если для любой пары точек х и х', а Ј х < х' Ј b выполняется неравенство f (x) Ј f (x'), и строго возрастающей — если выполняется неравенство f (x) < f (x'). Аналогично определяется убывание и строгое убывание функции. Например, функция у = х2 (рис., а) строго возрастает на отрезке [0,1], а


(рис., б) строго убывает на этом отрезке. Возрастающие функции обозначаются f (x), а убывающие f (x)Ї. Для того чтобы дифференцируемая функция f (x) была возрастающей на отрезке [а, b], необходимо и достаточно, чтобы её производная f'(x) была неотрицательной на [а, b].
Наряду с возрастанием и убыванием функции на отрезке рассматривают возрастание и убывание функции в точке. Функция у = f (x) называется возрастающей в точке x0, если найдётся такой интервал (a, b), содержащий точку x0, что для любой точки х из (a, b), х> x0, выполняется неравенство f (x0) Ј f (x), и для любой точки х из (a, b), х< x0, выполняется неравенство f (x) Ј f (x0). Аналогично определяется строгое возрастание функции в точке x0. Если f'(x0) > 0, то функция f (x) строго возрастает в точке x0. Если f (x) возрастает в каждой точке интервала (a, b), то она возрастает на этом интервале.
Экстремум функции.
Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x1< x2 выполняется неравенство f(x1) < f (x2) (f(x1) > f(x2)).
Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f ' (x) > 0 (f ' (x) < 0).
Точка x0nназывается точкой локального максимума (минимума) функции f(x), если существует окрестность точки x0, для всех точек которой верно неравенство f(x) < f(x0 ) (f(x) > f(x0 )).
Точки максимума и минимума называются точками экстремума , а значения функции в этих точках - ее экстремумами.
Необходимые условия экстремума. Если точка x0 является точкой экстремума функции f(x), то либо f '(x0) = 0, либо f '(x0) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.
Первое достаточное условие экстремума. Пусть x0 - критическая точка. Если f ' (x) при переходе через точку x0 меняет знак плюс на минус, то в точке x0 функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x0 экстремума нет.
Второе достаточное условие экстремума. Пусть функция f(x) имеет производную f '(x) в окрестности точки x0и вторую производную f ''(x0) в самой точке x0. Если f '(x0) = 0, f''(x0)>0, (f''(x0)<0), то точка x0 является точкой локального минимума (максимума) функции f(x). Если же f''(x0)=0, то нужно либо пользоваться первым достаточным условием экстремума, либо привлекать высшие производные.
На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
Наибольшее и наименьшее значение функции на интервале и на отрезке
Вывод
уравнения
касательной
к
параболе.
Свойство
выпуклого
параболического
зеркала.
Общее
уравнение
линий
второго
порядка
и
его
частные
случаи.
Плоскость
в
пространстве.
Различные
виды
уравнения
плоскости.
Угол
между
двумя
плоскостями,
условия
параллельности
и
перпендикулярности
двух
плоскостей.
Расстояние
от
точки
до
плоскости. 
 8
вопрос:
вогнутость
и
выпуклость
графиков
функции,
точки
перегиба
8
вопрос:
вогнутость
и
выпуклость
графиков
функции,
точки
перегиба
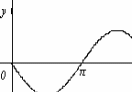
График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).
Примеры.
Полуокружность
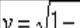 выпукла
на
[–1; 1].
выпукла
на
[–1; 1].Парабола y = x2 вогнута на интервале (-?; +?).
График функции в одних интервалах может быть выпуклым, а в других вогнутым. Так график функции y = sin x на [0,2; π], выпуклый в интервале (0; π) и вогнутый в (π; 2π).
Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым.
Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x)отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.
Доказательство. Предположим для определенности, что f''(x) < 0 и докажем, что график функции будет выпуклым.
Возьмем
на
графике
функции y
= f(x) произвольную
точку M0 с
абсциссой x0 ? (a; b)
и
проведем
через
точку M0 касательную.
Ее
уравнение ![]() .
Мы
должны
показать,
что
график
функции
на (a;
b) лежит
ниже
этой
касательной,
т.е.
при
одном
и
том
же
значении x ордината
кривой y
= f(x) будет
меньше
ордината
касательной.
.
Мы
должны
показать,
что
график
функции
на (a;
b) лежит
ниже
этой
касательной,
т.е.
при
одном
и
том
же
значении x ордината
кривой y
= f(x) будет
меньше
ордината
касательной.
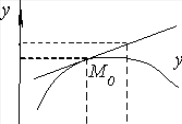
Итак,
уравнение
кривой
имеет
вид y
= f(x).
Обозначим ![]() ординату
касательной,
соответствующую
абсциссе x.
Тогда
ординату
касательной,
соответствующую
абсциссе x.
Тогда ![]() .
Следовательно,
разность
ординат
кривой
и
касательной
при
одном
и
том
же
значении x будет
.
Следовательно,
разность
ординат
кривой
и
касательной
при
одном
и
том
же
значении x будет ![]() .
.
Разность f(x)
– f(x0) преобразуем
по
теореме
Лагранжа ![]() ,
где c между x и x0.
,
где c между x и x0.
Таким образом,
![]() .
.
К
выражению,
стоящему
в
квадратных
скобках
снова
применим
теорему
Лагранжа: ![]() ,
где c1 между c0 и x0.
По
условию
теоремы f ''(x)
< 0. Определим
знак
произведения
второго
и
третьего
сомножителей.
,
где c1 между c0 и x0.
По
условию
теоремы f ''(x)
< 0. Определим
знак
произведения
второго
и
третьего
сомножителей.
Предположим, что x>x0. Тогда x0<c1<c<x, следовательно,
 (x
– x0)
> 0 и
(c
– x0)
> 0. Поэтому
(x
– x0)
> 0 и
(c
– x0)
> 0. Поэтому 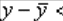 .
.Пусть x<x0, следовательно, x < c < c1 < x0 и (x – x0) < 0, (c – x0) < 0. Поэтому вновь .
Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x0 ? (a; b), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично.
Примеры.
Установить интервалы выпуклости и вогнутости кривой y = 2 – x2.
Найдем y '' и определим, где вторая производная положительна и где отрицательна. y' = –2x, y'' = –2 < 0 на (–?; +?), следовательно, функция всюду выпукла.
y = ex. Так как y'' = ex > 0 при любых x, то кривая всюду вогнута.

y = x3. Так как y'' = 6x, то y'' < 0 при x < 0 и y'' > 0 при x > 0. Следовательно, при x < 0 кривая выпукла, а при x > 0 вогнута.
Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.
Определим достаточные условия того, что данная точка кривой является точкой перегиба.
Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x= x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба.
Доказательство. Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0.
Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
Примеры. Найти точки перегиба и определить интервалы выпуклости и вогнутости кривых.
![]()
Найдем производные заданной функции до второго порядка.
![]() .
.
![]() .
Вторая
производная
не
существует
при x =
1. Исследуем
эту
точку
на
возможный
перегиб.
.
Вторая
производная
не
существует
при x =
1. Исследуем
эту
точку
на
возможный
перегиб.
Итак, точка перегиба x = 1. Функция выпукла на (1; +?), вогнута на (–?; 1).
2)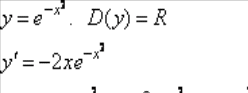
Возможные
точки
перегиба
найдем,
решив
уравнение
2x2 –
1 = 0. Отсюда ![]() .
Точки
перегиба
.
Точки
перегиба ![]() .
Функция
выпукла
на
.
Функция
выпукла
на ![]() и
вогнута
на
и
вогнута
на ![]() .
.
3)y =
ln (1 – x2).
Область
определения
функции D(y)
= (-1; 1).
![]() .
.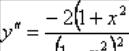 при
всех x из
(–1; 1).
при
всех x из
(–1; 1).
Следовательно, f(x) выпуклая
на
(–1; 1).



 9
вопрос:
асимптоты,
исследования
графиков
функции
Асимптотой
графика
функции у = f(x)
называется
прямая,
расстояние
от
которой
до
текущей
точки
графика
функции
стремится
к
нулю
при
неограниченном
удалении
этой
точки
от
начала
координат.
9
вопрос:
асимптоты,
исследования
графиков
функции
Асимптотой
графика
функции у = f(x)
называется
прямая,
расстояние
от
которой
до
текущей
точки
графика
функции
стремится
к
нулю
при
неограниченном
удалении
этой
точки
от
начала
координат.
Для
нахождения
вертикальных
асимптот,
то
есть
асимптот,
параллельных
оси OY,
надо
найти
точки
разрыва
функции II рода.
Если х0 –
такая
точка,
то
хотя
бы
один
из
пределов ![]() f(x)
или
f(x)
или ![]() f(x) равен
бесконечности.
Это
означает,
что
прямая х = х0 –
вертикальная
асимптота.
Если
функция
не
имеет
точек
разрыва II рода,
то
график
функции
не
имеет
вертикальных
асимптот.
f(x) равен
бесконечности.
Это
означает,
что
прямая х = х0 –
вертикальная
асимптота.
Если
функция
не
имеет
точек
разрыва II рода,
то
график
функции
не
имеет
вертикальных
асимптот.
Пусть
график
функции y = f(x)
имеет
невертикальную
асимптоту.
Уравнение
невертикальной
прямой
можно
записать
в
виде y = kx+b.
Пусть
М(х,у)
– текущая
точка
графика.
Опустим
из
точки
М
перпендикуляр
МN на
асимптоту.
Из
определения
асимптоты
следует: ![]() MN =
0. Из
?М1 MN получаем М1М
=
MN =
0. Из
?М1 MN получаем М1М
= ![]() , где ? –
угол
между
асимптотой
и
осью
ОХ.
Поскольку ? –
величина
постоянная,
то
, где ? –
угол
между
асимптотой
и
осью
ОХ.
Поскольку ? –
величина
постоянная,
то ![]() .
Заметим,
что М1М = РМ1-РМ = уасимпт.-уграфика = (kx+b)-f(x),
поэтому
.
Заметим,
что М1М = РМ1-РМ = уасимпт.-уграфика = (kx+b)-f(x),
поэтому ![]() Последнее
равенство
означает,
что
функция
Последнее
равенство
означает,
что
функция ![]() является
бесконечно
малой
при
является
бесконечно
малой
при ![]() .
Разделим
обе
части
последнего
равенства
на х и
перейдем
к
пределу
при
.
Разделим
обе
части
последнего
равенства
на х и
перейдем
к
пределу
при ![]() ,
получим
,
получим ![]() .
Так
как
.
Так
как ![]()
![]()

Определим
теперь b.
Так
как ![]() то
то ![]() Переходя
к
пределу
при
,
получаем
Переходя
к
пределу
при
,
получаем
![]()
Если k или b не существуют, то график функции не имеет невертикальной асимптоты.
В
частном
случае
при k =
0 получается
горизонтальная
асимптота.
Аналогично
находят
асимптоты
при x![]() .
График
может
иметь
различные
асимптоты
при
и x
или
иметь
только
одну
из
них.
.
График
может
иметь
различные
асимптоты
при
и x
или
иметь
только
одну
из
них.
Общие исследование функции y = f(x).
Область определения функции. Найти ее область определения D(f) . Если это не слишком сложно, то полезно найти также область значений E(f) . (Однако, во многих случаях, вопрос нахождения E(f) откладывается до нахождения экстремумов функции.)
Особые свойства функции. Выяснить общие свойства функции: четность, нечетность, периодичность и т.п. Не любая функция обладает такими свойствами, как четность либо нечетность. Функция заведомо не является ни четной, ни нечетной, если ее область определения несимметрична относительно точки 0 на оси Ox. Точно так же, у любой периодической функции область определения состоит либо из всей вещественной оси, либо из объединения периодически повторяющихся систем промежутков.
Вертикальные асимптоты. Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определения D(f), если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она не определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.
Наклонные и горизонтальные асимптоты. Если область определения D(f) вклоючает в себя лучи вида (a;+) или (?;b), то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при x+ или x? соответственно, т.е. найтиlimxf(x). Наклонные асимптоты: y = kx + b, где k=limx+xf(x) иb=limx+(f(x)?x). Горизонтальны асимптоты: y = b, где limxf(x)=b.
Нахождение точек пересечения графика с осями. Нахождение точки пересечения графика с осью Oy. Для этого нужно вычислить значение f(0). Найти также точки пересечения графика с осью Ox, для чего найти корни уравнения f(x) = 0 (или убедиться в отсутствии корней). Уравнение часто удается решить лишь приближунно, но уже отделение корней помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва.
Нахождение точек пересечения графика с асимптотой. В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой.
10 вопрос: производная показательно степенной функции Производная показательно-степенной функции.
Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной.
Пусть u = f(x) и v = g(x) – функции, имеющие производные в точке х, f(x)>0.
Найдем производную функции y = uv. Логарифмируя, получим:
lny = vlnu
Пример. Найти производную функции .
По полученной выше формуле получаем:
Производные этих функций:
Окончательно:
