Когерентность. Длина и ширина когерентности.

Когерентностью называется согласованное протекание нескольких колебательных или волновых процессов. Строго когерентными могут быть только монохроматические волны, то есть волны с постоянной амплитудой, частотой и направлением распространения, то есть гармонические волны, описываемые уравнением: . Поэтому разность фаз двух монохроматических волн одинаковой частоты в каждой точке остается постоянной. Пусть в некоторой точке пространства колебания возбуждаются сложением двух монохроматических волн одинаковой частоты и одинакового направления колебания:

, .Тогда амплитуда результирующего колебания в данной точке может быть рассчитана как: , где  = ₂ – ₁ – разность фаз между двумя колебаниями. В случае когерентных волн разность фаз имеет постоянное во времени значение (но свое для каждой точки). В соответствии с этим амплитуда результирующего колебания изменяется в пространстве вместе с изменением разности фаз. Поскольку интенсивность пропорциональна квадрату амплитуды, то амплитуда также меняется в зависимости от разницы фаз колебаний: . Последнее слагаемое суммы носит название интерференционного члена. В тех точках пространства, где cos > 0, там I > I₁ + I₂; там же, где cos < 0, там I < I₁ + I₂. Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы. Это явление называется интерференцией волн. Особенно контрастно проявляется интерференция, когда интенсивность одинакова: I₁ = I₂. Тогда интенсивность в различных точках можно рассчитать как:

.В этом случае интенсивность изменяется от значения I = 4I₁ в максимумах до I = 0 в минимумах.

Для некогерентных волн интенсивность всюду одинакова и равна I = I₁ + I₂.

Билет№5

Сложение колебаний во взаимно перпендикулярных направлениях.

Рассмотрим тело, колеблющееся на плоскости с одинаковыми частотами во взаимно перпендикулярных направлениях. Примером может служить горизонтальное движение без трения груза, закрепленного на четырех одинаковых пружинах.Система отсчета выбрана так, что ее начало совпадает с положением тела в состоянии равновесия. Для того, чтобы заставить тело колебаться, оттянем его на какое-то расстояние A от положения равновесия и отпустим. Тогда тело будет совершать колебания с амплитудой A относительно положения равновесия. При этом координаты и колеблющегося тела будут изменяться по закону: , , где A_x – проекция амплитуды но ось X (рис. 3.7);

A_y – проекция амплитуды на ось Y; – циклическая частота совершаемых колебаний; – начальная фаза колебаний по оси X; – начальная фаза колебаний по оси Y.Получим уравнение, описывающее поведение колеблющейся частицы. С учетом того, что разность фаз складываемых колебаний , выражение можно представить в виде:

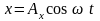, .Выясним, какой вид имеет зависимость между координатами x и y при таких колебаниях. Выразим и через отношение амплитуд и координат.

Из получаем:

Представим в эквивалентном виде:

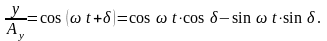Выражение для получим из :

Подставим в уравнения :

.Перенося слагаемые из правой части в левую, получим:

.Возведем в квадрат:

Преобразуем полученное выражение: Окончательно получаем уравнение движения частицы:

Очевидно, что в рассматриваемом случае траекторией частицы в общем случае будет являться эллипс, общий вид которого определяется разностью фаз и отношением амплитуд и .Рассмотрим некоторые частные случаи.

1. . В этом случае , . Уравнение колебания принимает вид:

,частица движется по прямой в первом и третьем квадрантах . При этом смещение относительно положения равновесия изменяется по закону:

,где A – амплитуда колебаний относительно положения равновесия:

.

2. . При такой разности фаз , . С учетом знака уравнение колебания тоже описывает прямую: , но частица движется по прямой уже во втором и четвертом квадрантах.

3. 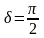. В этом случае уравнение колебания принимает вид:

,частица движется по эллипсу, полуоси которого и совпадают с осями координат. При = эллипс превращается в окружность радиуса R= = . Движение частицы по траектории будет происходить в направлении часовой стрелки . Направление движения можно определить в процессе построения графика функции – при увеличении времени t точки, по которым строится график функции будут перемещаться в том направлении, в котором движется колеблющаяся точка.

4. . То же самое, что и , так как изменение фазы на несущественно. Движение будет происходить по эллипсу, как и в случае 3, с той только разницей, что движение будет осуществляться против часовой стрелки.На практике добиться полного совпадения частот колебаний непросто, частоты всегда имеют небольшую разность (кроме электромагнитных колебаний, когда частота задается одним генератором, а потом колебания подаются на разные входы осциллографа).При относительно малом несовпадении частот, когда , возникает медленно меняющаяся дополнительная разность фаз между двумя колебаниями. При наблюдении сложения таких колебаний (при отношении частот ~1:1) на экране осциллографа видно, что фигура медленно вращается, последовательно проходя все фазы, показанные на рис.Рассмотрим полную энергию суммарного колебания, складывается из энергий каждого колебания:

,где E_x – энергия колебаний по оси X;

E_y – энергия колебаний по оси Y.В свою очередь, каждая из этих энергий состоит потенциальной и кинетической энергии:

Согласно энергия колебаний по осям X иY может быть представлена как

, ,где A_x – амплитуда колебаний по оси X;A_y – амплитуда колебаний по оси Y;ω_x – частота колебаний по оси X;ω_y – частота колебаний по оси Y, причем частоты могут не совпадать.Тогда полная энергия суммарного колебания: пропорциональна квадрату общей амплитуды, которая равна. .