Билет №1.

1. Периодические процессы. Гармонические колебания. Дифференциальное уравнение гармонического осциллятора и его решение.

Периодические процессы-изменение какой-либо величины повторяется в том же самом виде через совершенно определенное время–период. Математическое определение периодической функции такое:если f(t) есть периодическая функция от t с периодом T,то при любом t функция f(t)=f(t+T),т.е. полностью повторяет себя. Гармонические колебания относятся к так называемым периодическим процессам, то есть к таким процессам, при которых состояние системы полностью повторяется через строго одинаковые промежутки времени – период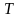 : 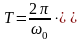.В случае с маятниками период колебаний можно определить как время, прошедшее между двумя максимальными отклонениями маятника в одну сторону. Единица измерения периода – секунда. 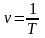Период определяет и другие характеристики колебания, такие как частота: и циклическая частота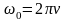 .Единицей измерения частоты является Герц, циклической частоты–радиан в секунду. Обычно радиан (как величина безразмерная)не указывается и поэтому за единицу измерения циклической частоты принимается с^-1. Тем не менее размерность единиц частоты и циклической частоты одна и та же: с^-1. Период колебаний можно выразить через вышеуказанные характеристики колебаний:На рис. показан график гармонических колебаний, описываемых формулой. Скорость движения материальной точки при колебаниях определяется производной от смещения точки (в данном случае – координаты x) по времени: 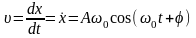Максимальное значение скорости: 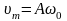называют амплитудой скорости. Аналогично определяется ускорение колеблющейся точки:

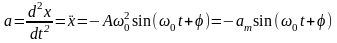
где амплитуда ускорения: 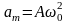Из уравнений и видно, что скорость и ускорение материальной точки также совершают гармонические колебания с частотой 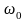. Для определения разности фаз между смещением точки, ее скоростью и ускорением представим выражения и в эквивалентном виде:

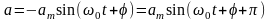Из сравнения полученных уравнений с (1.1) видно, что скорость опережает смещение 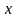по фазе на 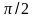, а ускорение – на 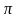, то есть находится в противофазе со смещением .Графики изменения скорости и ускорения со временем при гармонических колебаниях показаны на рис.

На рис. видно смещение фаз между скоростью и ускорением на , причем ускорение по фазе опережает скорость движения частицы.Проанализируем подробней уравнение. Из сравнения его с уравнением видно, что ,или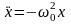 .Перенося все слагаемые влево, получаем уравнение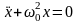 , называемое дифференциальным уравнением свободных гармонических колебаний. Свободные гармонические колебания также называют просто гармоническими колебаниями, а уравнение – дифференциальным уравнением гармонических колебаний (или дифференциальным уравнением гармонического осциллятора).

Зная зависимость между смещением и скоростью при гармонических колебаниях, можно найти остальные параметры колебаний, такие, как амплитуда A и начальная фаза 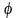.Обозначим как x₀ положение колеблющейся точки в момент времени t=0 (на рис. выбрано значение x₀=0).

Величину скорости в момент времени t=0 обозначим как υ₀. Значения x₀ и υ₀ называются начальными условиями:

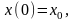
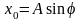Подставляя t=0 и x₀ в уравнение получим: .Подставляя t=0 и 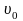в уравнение получим: 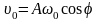.Тогда из и находим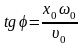 ,откуда получаем выражение для начальной фазы: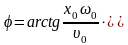 Для нахождения амплитуды из (1.16) и (1.17) найдем 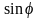и :

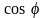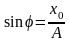, Складывая квадраты выражений и получаем:

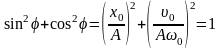,откуд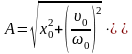а Таким образом, зная начальные условия, можно найти значения амплитуды A и начальной фазы .Механические гармонические колебания являются результатом двух свойств системы: действия возвращающей силы и инерции.Инерция противодействует изменению положения тела (или его скорости), возвращающая сила направлена в сторону, противоположную смещению тела.

Действие возвращающей силы рассмотрим на примерах механических осцилляторов.