Статические моменты сечения

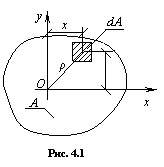
Статическим моментом плоского сечения относительно некоторой оси называется, взятая по всей его площади А, сумма произведений площадей элементарных площадок dA на их расстояния от этой оси (рис. 4.1):

 

; (3)

(4)

(5)

где y_c – расстояние от центра тяжести всего плоского сечения до оси x; x_c – расстояние от центра тяжести всего сечения до оси y.

Статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси:

(6)

В формулах (6) введены обозначения: А₁, А₂, …, А_n – площади простых элементов, составляющих плоское сложное сечение; x₁, y₁, x₂, y₂, x₃, y₃, … , x_n, y_n – координаты центров тяжести простых составляющих сложного плоского сечения относительно выбранных осей х и у.

Из выражений (4) можно определить координаты центра тяжести плоского сечения:

(7)

Для сложного поперечного сечения формулы (7) можно представить в следующем виде

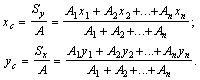
Осевым моментом инерции сечения (second moment of area или second moment of inertia) относительно оси x называется сумма произведений элементарных площадок dA на квадрат их расстояний до данной оси, численно равная интегралу

Jx= Ay2dA 

И относительно оси y:

Jy= Ax2dA 

23) Моменты инерций относительно параллельных осей.Поворот осей

Пусть известны моменты инерции фигуры относительно центральных осей и :

; ; (2.12)

Требуется определить моменты инерции относительно осей, параллельных центральным (рис 2.5).

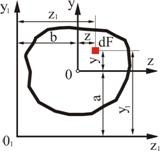
Рис. 2.5

; ; (2.13)

Координаты любой точки в новой системе можно выразить через координаты в старых осях так:

;

Подставим эти значения в формулы (2.13) и интегрируем почленно:

(2.14)

(2.15)

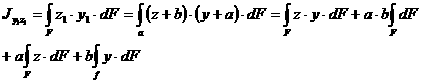(2.16)

Так как интегралы и равны нулю как статические моменты относительно центральных осей, то формулы (2.14) - (2.16) принимают вид

;

; (2.17)

Зависимости между моментами инерции при повороте координатных осей.

Пусть известны моменты инерции произвольной фигуры (рис. 2. 6) относительно координатных осей , :

; ; (2.18)

Повернем оси , на угол против часовой стрелки, считая угол поворота осей в этом направлении положительным.

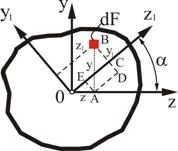
Рис. 2.6

Найдем теперь моменты инерции сечения относительно повернутых осей , :

; ; (2.19)

Координаты произвольной элементарной площадки в новой системе выражаются через координаты , прежней системы следующим образом:

(2.20)

(2.21)

Подставив эти выражения в (2.19) окончательно получим:

(2.22)

(2.23)