Повторение испытаний

Если  производится несколько  испытаний (опытов), причем вероятность события в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события .      Формула Бернулли

где - вероятность появления события A ровно k раз при n независимых испытаниях; p - вероятность появления события A при каждом испытании.

     Вероятность того, что при этом событие A:

     1) наступит n раз: ;

     2) не наступит ни разу: ;

     3) наступит хотя бы один раз: ;

     4) наступит не более k раз: ;

     5) наступит не менее k раз: .

11. Локальная теорема Лапласа.

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)

Для определения значений φ(x) можно воспользоваться специальной таблицей.

11. Интегральная теорема Лапласа.

Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k₁ раз и не более k₂ раз, приближенно равна

P(k₁;k₂)=Φ(x'') - Φ(x')

Здесь

-функция Лапласа

Значения функции Лапласа находят по специальной таблице.

11. Асимптотическая формула Пуассона. Условия её применимости.

Теорема. Пусть проведено n повторных независимых испытаний, в каждом из

которых события А наступает с вер-тью р, причем

1)число испытаний достаточно велико (n100)

2)Величина =np10, тогда вер-ть Pm,n того, что в этих испытаниях событие А наступит m раз вычисл. по след. приближ. ф-ле:

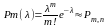
11. Понятие случайной величины. Дискретные и непрерывные случайные величины.

Пусть задано вероятностное пространство . Случайной величиной, заданной на этом пространстве, называется числовая функция , которая ставит в соответствие каждому элементарному исходу число - значение случайной величины на этом исходе. Данная функция должна быть -измеримой (где - борелевская сигма-алгебра на прямой), т.е. для любого борелевского множества его полный прообраз при отображении должен быть событием: .

Дискретные случайные величины

     Определение1: Случайная величина называется дискретной случайной величиной, если она принимает не более чем счетное число значений. Задание дискретной случайной величины по определению равносильно заданию закона распределения случайной величины в следующем виде:

    

Где

Следующее утверждение отражает связь между функцией распределения дискретной случайной величины и законом распределения случайной величины.

     Утверждение 1: Закон распределения и функция распределения дискретной случайной величины взаимно однозначно определяют друг друга.

Непрерывные случайные величины

     Определение 2: Распределение случайной величины называется непрерывным, а сама случайная величина - непрерывной случайной величиной, если для любого

,

где - интегрируемая по Лебегу функция. Функция называется плотностью распределения случайной величины .

     Теорема 1: Для того чтобы случайная величина была непрерывной случайной величиной, необходимо и достаточно, чтобы для любого

         (1)

     Замечание 1: Из представления (1) видно, что функция распределения непрерывной случайной величины является непрерывной функцией.

   

    Свойства плотности распределения:

1)

2) почти всюду.

3) для любых х, являющихся точками непрерывности плотности.

 

     Теорема 2: Для того, чтобы функция p = p(x) была плотностью распределения некоторой случайной величины , необходимо и достаточно, чтобы она удовлетворяла свойствам 1) и 2) плотности.

11. Закон распределения вероятностей дискретной случайной величины.

Так как дискретная случайная величина имеет конечное или счётное множество значений, то их можно просто перечислить и указать соответствующие вероятности. Это можно сделать, например, в форме таблицы

 

X	x1	x2	...	xn	...
P	p1	p2		pn

 

 где,  - вероятность того, что X примет значение x .

 

Такую таблицу называют рядом распределения.

События … несовместимы и в результате опыта одно из них обязательно происходит. Из этого следует

Примеры дискретных сл.вел:

1). Индикатор события I. Эта случайная величина имеет закон распределения : Если вероятность появления события   в некотором опыте равна p, то I принимает значение 1, если событие произошло, и значение 0, если событие не произошло. I можно назвать числом появлений события в одном опыте.

I	0	1
P	q	р

 

 

 

2). Гипергеометрический закон распределения. Возможные значения X: 0,1,…,n. И каждому значению X=m соответ­ствует вероятность P(X=m)=P = . Эта случайная величина, например, равна числу m бракованных изделий среди n взятых наугад из партии объёма N, содержащей M бракованных изделий.

3). Геометрический закон распределения.

X	1	2	3	…	n	…
P	p	qp		…		…

  q=1-p

Если, например, p – вероятность изготовления бракованной детали, то случайная величина X с этим законом распределения будет равна общему числу деталей     до момента изготовления первой бра­кованной детали.

Построение ряда распределения удобно лишь для дискретных случайных величин, так как можно перечислить их все возможные значения.

11. Биноминальное распределение.

Биномиальный закон распределения. Случайная величина может принимать значения 0,1,2,…,n и каждому значению X=m соответствует вероятность , где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону   можно назвать числом появле­нии события в n независимых опытах.

11. Распределение Пуассона.

Пуассоновский закон распределения. Случайная велbчина имеет возможные значения 0,1,2,3,…… и каждому значению Х=m со­ответствует вероятность ,где  - некоторый параметр.

11. Числовые характеристики дискретных случайных величин.

а) Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее значений на соответствующие им вероятности, т.е.:

или, если случайная величина может принимать счетное число значений, ,причем лишь в случае абсолютной сходимости ряда.