15)Затухающие колебания. Коэффициент затухания и логарифмический декремент затухания.

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, колебания будут затухать. В простейшем, и вместе с тем наиболее часто встречающемся, случае сила сопротивления пропорциональна величине скорости:

,

где r – постоянная величина, называемая коэффициентом сопротивления. Знак минус обусловлен тем, что сила и скорость имеют противоположные направления; следовательно, их проекции на ось X имеют разные знаки. Уравнение второго закона Ньютона при наличии сил сопротивления имеет вид: .

Применив обозначения  ,  , перепишем уравнение движения следующим образом:

.

Это уравнение описывает затухающие колебания системы. Коэффициент   называется коэффициентом затухания.

Экспериментальный график затухающих колебаний при малом коэффициенте затухания   представлен на рис. 7.6. Из рис. 7.6 видно, что график зависимости   выглядит как косинус, умноженный на некоторую функцию, которая убывает со временем. Эта функция представлена на рисунке штриховыми линиями. Простой функцией, которая ведет себя подобным образом, является экспоненциальная функция  . Поэтому решение можно записать в виде:

,

где   – частота затухающих колебаний.

Величина x периодически проходит через нуль и бесконечное число раз достигает максимума и минимума. Промежуток времени между двумя последовательными прохождениями   через нуль равен  . Удвоенное его значение  называется периодом колебаний.

Множитель  , стоящий перед периодической функцией  , называется амплитудой затухающих колебаний. Она экспоненциально убывает со временем. Скорость затухания определяется величиной  . Время, по истечении которого амплитуда колебаний уменьшается в   раз, называется временем затухания  . За это время система совершает   колебаний.

16)Энергия гармонических и затухающих колебаний.

Гармонические колебания - выполняется закон сохранения механической энергии: сумма кинетической и потенциальной энергий остается неизменной:

Пусть колебание происходит по закону синуса , тогда скорость меняется по закону косинуса . Запишем выражение для кинетической энергии:  .

Согласно закону сохранения энергии, полная энергия будет равна максимальной кинетической, т.к. в положении равновесия потенциальная равна нулю. Тогда:  . Для потенциальной энергии получим: 

Затухающими наз. колебания, энергия (а значит, и амплитуда) которых уменьшается с течением времени. Затухание свободных механических гармонических колебаний связано с убыванием механической энергии за счет действия сил сопротивления и трения.

Если сила сопротивления пропорциональна скорости относительного движения , то амплитуда колебаний изменяется по закону , где x0 – начальная амплитуда,  -

 

коэффициент затухания, характеризующий быстроту убывания амплитуды, e– основание натурального логарифма.

17)Вынужденные колебания. Резонанс.

В случае вынужденных колебаний система колеблется под действием внешней (вынуждающей) силы, и за счет работы этой силы периодически компенсируются потери энергии системы. Частота вынужденных колебаний (вынуждающая частота) зависит от частоты изменения внешней силы Определим амплитуду вынужденных колебаний тела массой m, считая колебания незатухающими вследствие постоянно действующей силы   .

Пусть эта сила изменяется со временем по закону   , где   амплитуда вынуждающей силы   . Возвращающая сила   и сила сопротивления   Тогда второй закон Ньютона можно записать в следующем виде: или

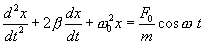
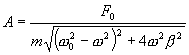
При циклической частоте вынуждающей силы ω=0 амплитуда колебаний   . В этом случае колебания не совершаются и смещение при вынужденных колебаниях равно статической деформации под действием постоянной силы F0:

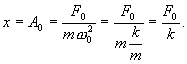
Поэтому отклонение A0 иногда называют статической амплитудой.

Если нет диссипации т.е β=0, то амплитуда колебаний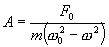

растет с увеличением циклической частоты ω вынуждающей силы Fвн и при   становится бесконечно большой (рис. 7.10). При дальнейшем росте циклической частоты ω амплитуда А вынужденных колебаний уменьшается, причем

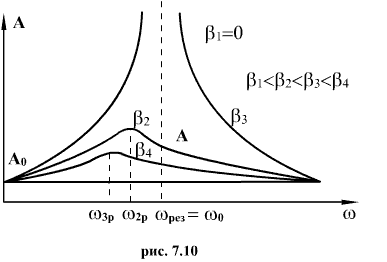
Явление резкого возрастания амплитуды вынужденных колебаний при приближении вынуждающей частоты ω к частоте собственных колебаний системы   называется резонансом.