
- •1)Система отсчета. Материальная точка. Радиус-вектор и вектор перемещения, их связь с координатами точки. Траектория.
- •2)Средняя и мгновенная скорости. Ускорения. Закон равноускоренного движения.
- •3)Движения тела по окружности. Угловая скорость, нормальное и тангенциальное ускорение. Движение по криволейной траектории.
- •4)Инерциальные системы отсчета, первый закон Ньютона.
- •5)Масса и импульс материальной точки. Сила. Второй закон Ньютона.
- •6)Третий закон Ньютона. Преобразования Галилея.
- •7)Замкнутая система материальных точек. Закон сохранения импульса.
- •8)Центр масс, система центра масс.
- •9)Момент импульса, закон сохранения момента импульса.
- •10)Работа и мощность силы. Средняя и мгновенная мощность.
- •11)Консервативные силы, работа консервативных сил.
- •12)Потенциальная энергия. Закон сохранения механической энергии.
- •13)Упругие и квазиупругие силы. Закон Гука. Гармонические колебания: частота, период, амплитуда и фаза колебаний.
- •14)Дифференциальное уравнение гармонических колебаний. Гармонические колебания пружинного и математического маятников.
- •15)Затухающие колебания. Коэффициент затухания и логарифмический декремент затухания.
- •16)Энергия гармонических и затухающих колебаний.
- •17)Вынужденные колебания. Резонанс.
- •18)Основные положения молекулярно-кинетической теории. Масса и размеры молекул.
- •19)Термодинамическая система и параметры её состояния.
- •20)Связь кинетической энергии молекул газа с температурой и давлением.
- •21)Равнораспределение энергии по степеням свободы.
- •22)Число степеней свободы и средняя энергия многоатомной молекулы.
- •23)Внутреняя энергия термодинамической системы.Теплоёмкость.
- •24)Работа, совершаемая газом при изменении объема.
- •25)Распределение молекул газа по скоростям. Функция распределения и её нормировка. Функция распределения Максвелла.
- •26)Наиболее вероятная, средняя и средне-квадратичная скорости молекул.
- •27)Опыт Штерна
- •28)Опыт Ламмерта
- •29)Идеальный газ в поле сил тяжести, барометрическая формула. Распределения Больцмана.
- •30)Основы термодинамики.
- •31)Тепловые двигатели и их кпд.
- •32)Адиабатический процесс. Работа газа при различных процессах.
- •33)Круговой процесс. Цикл Карно. Кпд цикла Карно.
- •34)Уравнения состояния идеальных газов. Уравнение Ван-дер-Ваальса.
- •35)Приведенная теплота. Энтропия.
- •36)Изменения энтропии в изопроцессах.
- •37)Свободная и связанная энергии.
- •38)Статистический смысл энтропии.
13)Упругие и квазиупругие силы. Закон Гука. Гармонические колебания: частота, период, амплитуда и фаза колебаний.
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.
При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
Fx = Fупр = –kx
Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела.
Силы иной природы, чем упругие, но в которых выполняется условие F = -kx, называются квазиупругими.
Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением x = xm cos (ωt + φ0)
Здесь x –
смещение тела от положения равновесия, xm –
амплитуда колебаний, т. е. максимальное
смещение от положения равновесия, ω –циклическая
или круговая частота колебаний, t –
время. Величина, стоящая под знаком
косинуса φ = ωt + φ0 называется фазой гармонического
процесса. При t = 0 φ = φ0,
поэтому φ0 называют начальной
фазой. Минимальный интервал времени,
через который происходит повторение
движения тела, называется периодом
колебаний T. Физическая величина,
обратная периоду колебаний,
называется частотой колебаний: 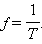
Частота
колебаний f показывает, сколько колебаний
совершается за 1 с. Единица частоты –
герц (Гц). Частота колебаний f связана с
циклической частотой ω и периодом
колебаний T соотношениями:
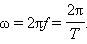
14)Дифференциальное уравнение гармонических колебаний. Гармонические колебания пружинного и математического маятников.
Дифференциальное уравнение гармонических колебаний материальной точки
![]() , или
, или ![]() , где m — масса точки; k — коэффициент
квазиупругой силы
, где m — масса точки; k — коэффициент
квазиупругой силы
Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.
![]() -
циклическая частота при колебаниях
пружинного маятника.
-
циклическая частота при колебаниях
пружинного маятника.
Период
колебаний 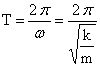 или
или ![]() (формула
Гюйгенса).
(формула
Гюйгенса).
Аналогичные
вычисления можно проделать с помощью
закона сохранения энергии. Учтем, что
потенциальная энергия упруго
деформированного тела равна![]() ,
а полная механическая энергия
равна максимальной потенциальной
или кинетической.
,
а полная механическая энергия
равна максимальной потенциальной
или кинетической.
![]() -
ускорение тела, колеблющегося на пружине,
не зависит от силы тяжести, действующей
на это тело. Сила тяжести только приводит
к изменению положения равновесия.
-
ускорение тела, колеблющегося на пружине,
не зависит от силы тяжести, действующей
на это тело. Сила тяжести только приводит
к изменению положения равновесия.
Выразим
ускорение:![]() .
.
Математический маятник это идеализированная система, представляющая собой материальную точку, подвешенную на тонкой, невесомой и нерастяжимой нити.
Математический маятник представлен на рисунке:
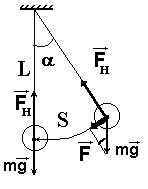
Математический маятник
Принцип действия математического маятника заключается в том, что при отклонении материальной точки от положения равновесия на малый угол a, такой, чтобы выполнялось условие sina=a, на тело будет действовать сила F = -mgsina = -mga. Знак минус указывает, что сила направлена в сторону, противоположную смещению. Сила F пропорциональна смещению S, следовательно, под действием этой силы материальная точка будет совершать гармонические колебания.
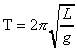 -
период колебания математического
маятника.
-
период колебания математического
маятника.
![]() -
уравнение движения математического
маятника.
-
уравнение движения математического
маятника.
![]() -
частота математического маятника.
-
частота математического маятника.
