10)Работа и мощность силы. Средняя и мгновенная мощность.

Изменение механического движения и энергии тела происходит в процессе силового взаимодействия этого тела с другими телами. Для количественной характеристики этого процесса в механике вводят понятие работы, совершаемой силой.

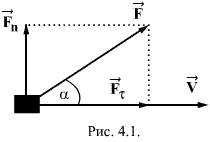
Если рассматриваемая сила   постоянна,а тело, к которому она приложена, движется поступательно и прямолинейно, то работой, совершаемой силой   при прохождении телом пути  , называют величину

где а - угол между силой   и направлением движения тела.

Работа - скалярная величина. Если вектор силы и вектор перемещений образуют острый угол т.е.  , то  , если  , то  , т.е. сила, действующая перпендикулярно к перемещению тела, работы не совершает.

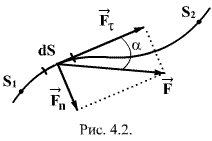
В общем случае тело может двигаться произвольным, достаточно сложным образом (рис.4.2). Выделим элементарный участок пути  , на котором силу можно считать постоянной и перемещение прямолинейным. Элементарная работа на этом участке равна

Полная работа на пути  определяется интегралом

Величина, характеризующая скорость совершения работы, называется мощностью Мощность численно равна отношению   к промежутку времени   за который она совершается.

или в общем случае ,

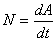Подставляя значение   получим

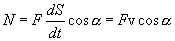
11)Консервативные силы, работа консервативных сил.

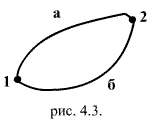
Силу  , действующую на материальную точку, называют консервативной или потенциальной, если работа  , совершаемая этой силой при перемещении этой точки из произвольного положения 1 в другое 2, не зависит от того, по какой траектории это перемещение произошло:

Изменение направления движения точки вдоль траектории на противоположное вызывает изменение знака консервативной силы, так как величина   меняет знак. Поэтому при перемещении материальной точки вдоль замкнутой траектории  , например  , работа консервативной силы равна нулю.

Примером консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия заряженных тел. Поле, работа сил которого по перемещению материальной точки вдоль произвольной замкнутой траектории равна нулю, называется потенциальным.

12)Потенциальная энергия. Закон сохранения механической энергии.

Потенциальная энергия - это энергия, обусловленная взаимным расположением тел и характером их взаимодействия. При соответствующих условиях возможно изменение потенциальной энергии, за счет чего совершается работа. Для поднятия тела массой m на высоту   необходимо совершить работу против сил тяготения Р: ,

знак минус перед интегралом, т.к. сила Р направлена в сторону противоположную изменению h.

Проинтегрируем это выражение:

Эта энергия пойдет на увеличение энергии замкнутой системы тело-Земля т.е. численно равна

Считая поверхности Земли  , получим

Эта энергия  системы тело - Земля и является потенциальной энергиейтела, поднятого на высоту h:

Величина 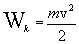называется кинетической энергией материальной точки. Таким образом, кинетическая энергия материальной точки – это энергия, которой обладает эта точка вследствие своего движения.

Рассмотрим процесс изменения состояния тела, поднятого на высоту h. При этом его потенциальная энергия

Тело начало свободно падать  . Из кинематики известно, что момент достижения поверхности земли оно будет иметь скорость   икинетическую энергию:

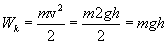
Кинетическая энергия тела, упавшего с высоты h, оказалась равной его потенциальной энергии, которую оно имело до начала падения. Следовательно:

На поверхности Земли h=0 и потенциальная энергия  , а  -максимальна. В начале падения  , а  т.е. потенциальная энергия переходит (превращается) в кинетическую. Таким образом, при падении тела в системе тело-Земля кинетическая энергия возрастает и, следовательно, ее изменение   равное работе  , имеет положительный знак, т.е.

Потенциальная энергия - уменьшается, и, следовательно, ее изменение имеет знак минус. Поэтому можем записать:

Сложив 2 уравнения сверху, получаем: или 

Сумма   представляет собой полную энергию, и, следовательно,

, а

Таким образом, энергия замкнутой консервативной системы остается постоянной при всех, происходящих в ней процессах и превращениях. Энергия может переходить из одних видов в другие (механические, тепловые, и т.д.), но общее ее количество остается постоянным. Данное положение называют законом сохранения и превращения энергии.