6)Третий закон Ньютона. Преобразования Галилея.

Третий закон Ньютона формулируется следующим образом:

Две материальные точки действуют друг на друга с силами, которые численно равны между собой и направлены во взаимно противоположные стороны вдоль прямой, соединяющей эти точки:

Следует отметить, что силы  и   приложены к разным телам и поэтому не уравновешивают друг друга.

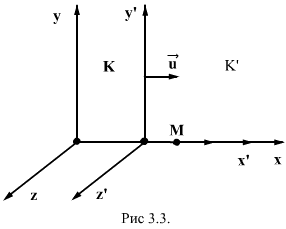Рассмотрим две системы отсчета: неподвижную (К) и движущуюся относительно первой вдоль оси Х с постоянной Х с постоянной скоростью   (K’). Координаты тела М в системе К x:y:z , а в системе К’ - x’:y’:z’. Эти координаты связаны между собой соотношениями, которые называются преобразованием Галилея

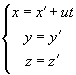
Дифференцируя эти уравнения по времени и учитывая, что  , найдем соотношения между скоростями и ускорениями:

Таким образом, если в системе К тело имеет ускорение а, то такое же ускорение оно имеет и в системе К’.

Согласно второму закону Ньютона:

т.е. второй закон Ньютона одинаков в обоих случаях.

При   движение по инерции, т.о., справедлив и первый закон Ньютона, т.е. рассматриваемая нами подвижная система является инерциальной. Следовательно, уравнения Ньютона для материальной точки, а также для произвольной системы материальных точек одинаковы во всех инерциальных системах отсчета - инвариантны по отношению к преобразованиям Галилея. Этот результат называется механическим принципом относительности (принцип относительности Галилея), и формулируется следующим образом: равномерное и прямолинейное движение (относительно какой-либо инерциальной системы отсчета) замкнутой системы не влияет на закономерности протекания в ней механических процессов. Следовательно, в механике все инерциальные системы отсчета совершенно равноправны. Поэтому никакими механическими опытами внутри системы нельзя обнаружить движется ли система равномерно и прямолинейно или покоится.

7)Замкнутая система материальных точек. Закон сохранения импульса.

Совокупность материальных точек (тел), рассматриваемых как единое целое, называетсямеханической системой. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы (они взаимно уравновешиваются), называется замкнутой или изолированной. В такой системе необходимо учитывать только силы взаимодействия между входящими в нее телами (внутренние силы). Строго говоря, изолированных механических систем в природе не существует.       Рассмотрим изолированную механическую систему, состоящую из n тел с массами m₁, m₂, …, m_n. Обозначим скорости этих тел через v₁, v₂, …, v_n а внутреннюю силу, действующую на i-е тело со стороны k-го,- через F_ik.

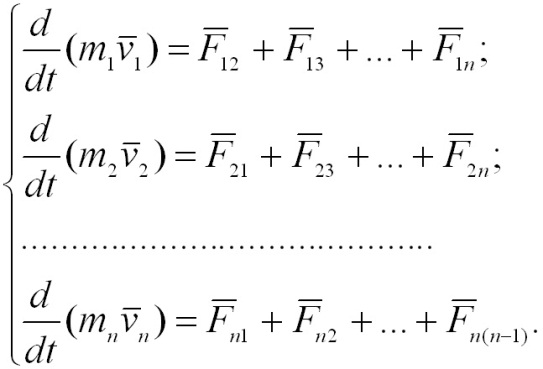
      Складывая почленно эти уравнения и группируя силы F_ik и F_ki, получим:

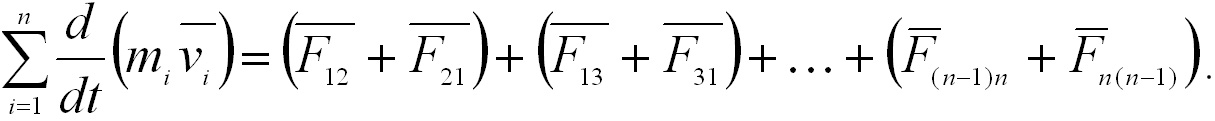
      Согласно третьему закону Ньютона F_ik = -F_ki, поэтому все скобки в правой части этого уравнения равны нулю, т.е.

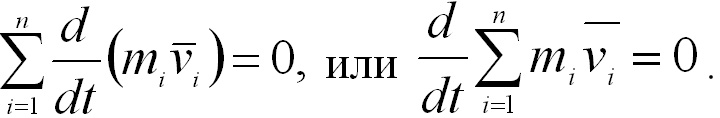
      Векторная сумма   представляет собой импульс всей системы. Таким образом, 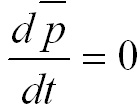  или                                                                                              (2.9)       Выражение (2.9) представляет собой закон сохранения импульса: импульс замкнутой системы тел с течением времени не изменяется.       Закон сохранения импульса справедлив не только в классической механике; он выполняется и для замкнутых систем микрочастиц, т.е. действует и в квантовой механике. Другими словами, этот закон носит универсальный характер и является фундаментальным законом природы.