15. Проецирование. Общий вид преобразований в пространстве. Виды проекций.

Трехмерных объекты, на бумаге и на экране дисплея, вычерчиваются при помощи двухмерных проекций. В плоской проекции каждая точка предмета отображается определенным образом на плоскость проекции, и её образ называется точкой проекции. Если линии, соединяющие точки предмета с соответствующими точками отображения, параллельны, то мы имеем плоскую параллельную проекцию. Если же линии сходятся в одной общей точке, то получаемое изображение называется центральной проекцией, или перспективным изображением предмета.

Проецирование эквивалентно сдвигу картинной плоскости и предмета до тех пор, пока плоскость проекции не пройдет через начало координат. Чтобы восстановить точку объекта, необходимо выполнить обратные преобразования.

Общая формула преобразования

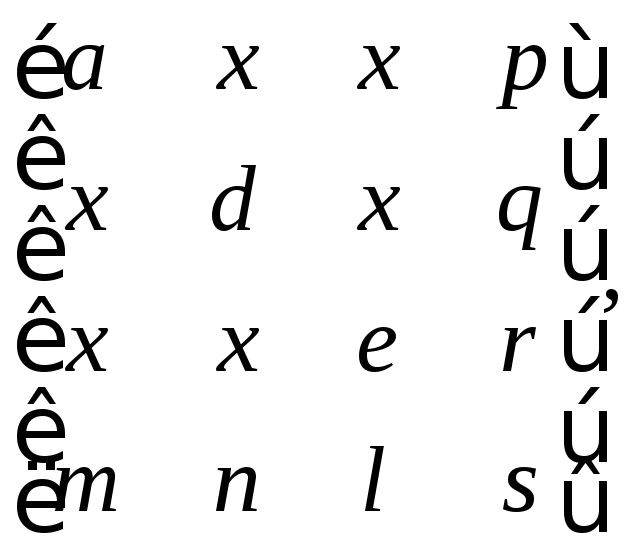
где a, d, е – масштабирование: m, n, l – смещение; p, q, r – проецирование; s – комплексное масштабирование; х – вращение.

Параллельные проекции можно разделить на следующие группы:

1) ортографическая проекция (параллельно одной из координатных плоскостей) координатная плоскость параллельна или совпадает с одной из координатных плоскостей. Если она параллельна, то необходимо координаты исходной точки умножить на матрицу сдвига с параметром m или n или l <>0.

2) аксонометрическая проекция (проектирующие прямые перпендикулярны картинной плоскости):

• триметрическая (нормальный вектор картинной плоскости образует с ортами координатных осей попарно различные углы);

• диметрическая (два угла между нормалью картинной плоскости и координатными осями равны);

– изометрическая (три угла между нормалью картинной плоскости и координатными осями равны); Каждый из трех видов аксонометрических проекций получается комбинацией поворотов, за которой следует параллельное проектирование. Например, поворот вокруг оси ординат, оси абцисс и проектирование вдоль оси аппликат.

3) Проекции, для получения которых используется пучок прямых, не перпендикулярных плоскости экрана, называют косоугольными.

• свободная;

• кабинетная.

Среди перспективных проекций выделяются:

• одноточечная (r  0);

• двухточечная (p, q  0);

• трехточечная (p, q, r  0).

На фотографиях, картинах, экране изображения кажутся нам естественными и правильными. Такие проекции называют перспективными. Одно из их основных свойств – более удаленные предметы изображаются в меньших масштабах, а параллельные прямые, в общем случае, не параллельны. Обычная перспективная проекция – это центральная проекция на плоскость прямыми лучами, проходящими через точку – центр проецирования. Один из проецирующих лучей перпендикулярен к плоскости проецирования и называется главным. Точка пересечения этого луча и плоскости проекции – главная точка картины.

Когда нужно показать широкую панораму или окружающее нас пространство, плоская картина становится неэффективной. Можно представить себе зрителя окруженным цилиндрической или сферической (полусферической) поверхностью, на которую нанесено изображение. Чтобы на экране изображение воспринималось правильным, на пленке оно должно быть построено по специальным алгоритмам. Такие разнообразные проекции называются специальными.

В OpenGL ортографическая проекция задается функциями:

• glOrtho(left, right, bottom, top, near, far), где near >0, far >0.

• glOrtho2D(left, right, bottom, top), где near=0, far=1.

В OpenGL перспективная проекция задается функциями:

• glFrustum(left, right, bottom, top, near, far), где near >0 , far >0;

• gluPerespective(fovy,aspect,near,far) – параметр fovy задает угол видимости в направлении оси OY в градусах, центрированный относительно этой оси.

Используемый в OpenGL и других графических API подход базируется на методике нормализации проецирования (projection normalization), которая предусматривает сведение всех типов проекций к ортогональной, для чего выполняется предварительной искажение исходных объектов.