Пересечение луча с плоскостью и многоугольником Вопрос 32

Пересечение луча с плоскостью

Пусть плоскость задана общим уравнением:

где N=(A, B, C) — нормальный вектор плоскости.

Заменяя в уравнении плоскости величины x, y и z их выраже­ниями, получим линейное уравнение относительно t:

Разрешая его, находим, что

Если

(a обращается в нуль), то луч паралле-

лен плоскости и, следовательно, не пересекает ее.

В случае t*<0 луч не пересекает плоскости.

Если t*>0 то координаты точки пересечения вычисляются под­становкой в выражения полученного значения

Пересечение луча с многоугольником

В данном случае задача разбивается на две:

1) нахождение пересечения луча с плоскостью, в которой лежит многоугольник;

2) проверка принадлежности точки пересечения многоугольни­ку.

Решение первой части задачи рассмотрено в предыдущем разде­ле. Остается проверить принадлежность полученной точки много­угольнику.

Решение будет состоять из следующих шагов:

• нахождения пересечения плоскости треугольника с отрезком;

• проверки: лежит ли точка пересечения внутри треугольника. Нахождение точки пересечения луча с плоскостью рассмотрено

в предыдущем разделе. Проверим, лежит ли полученная точка внутри треугольника.

Способ, которым мы воспользуемся, опирается на то, что сумма внутренних углов вида "вершина-точка-вершина" равна 2π, если точ­ка внутри треугольника. Для точки вне треугольника эта сумма будет меньше. Очевидно, сумма берется для одной точки — точки пересече­ния линии и плоскости, и по всем сочетаниям вершин.

Если мы вычислим единичные векторыP_a1, P_a2, P_a3

тогда углы будут равны

Пересечение луча с прямоугольным параллелепипедом. Вопрос33

Прямоугольный параллелепипед со сторонами, параллельными координатным плоскостям, однозначно определяется любыми двумя своими вершинами, примыкающими к одной из его диагоналей.

Пусть прямоугольный параллелепипед задан вершинами

При l = 0 луч параллелен этим плоскостям и, если X₀=x_- или X₀=x₊, не пересекает рассматриваемый прямоугольный па­раллелепипед. Если же луч непараллелен этим плоскостям, то вычисляем отношения:

Можно считать, что t_1x <t_2x (в противном случае меняем их мес­тами). Положим t_near=t_1x, t_far=t_2x

Считая, что m не равно нулю, и рассматривая вторую пару плос­костей, несущих грани заданного параллелепипеда, y=y_-_ и y=y₊, нахо­дим величины

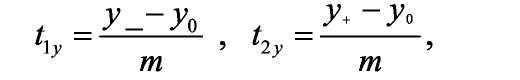
если t_1y<t_near , полагаем t_near =t _1y, если t_2y >t _far, полагаем t_far = t_2y, при

t_near >t_far ии при t_far<0 заданный луч проходит мимо прямоугольного параллелепипеда.

Считая, что n не равно нулю, рассматриваем последнюю пару плоскостей z=z_- и z=z₊ находим величины:

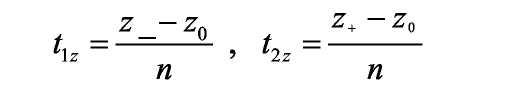
и повторяем предыдущие сравнения.

Если в итоге мы получим, что 0 < t_near <t _far или 0 < t_far, то задан­ный луч непременно пересечет исходный параллелепипед со сторо­нами, параллельными координатным осям.

Если луч проходит через прямоугольный параллелепипед (при этом считается, что начальная точка луча лежит вне параллелепипе­да), то расстояние от начала луча до точки его входа в параллелепи­пед равно t_near, а до точки выхода t_far соответственно.