17. Понятие автокорреляции. Тесты на наличие автокорреляции. Тест Бреуша-Годфри.

Автокорреляция- зависимость последующих уравнений ряда от предыдущих.

Тест серий (Бреуша—Годфри). Тест основан на следующей идее: если имеется корреляция между соседними наблюдениями, то естественно ожидать, что в уравнении

e =pe +v , t= 1, ..., n, (7.31) (где e — остатки регрессии, полученные обычным методом наименьших квадратов), коэффициент р окажется значимо отличающимсяот нуля.

Заметим, что уравнение (7.31) является авторегрессионным уравнением первого порядка (см. § 6.5).

Практическое применение теста заключается в оценивании методом наименьших квадратов регрессии (7.31)

Преимущество теста Бреуша—Годфри по сравнению с тестом Дарбина—Уотсона заключается в первую очередь в том, что он проверяется с помощью с т а т и с т и ч е с к о г о к р и т е рия, между тем как тест Дарбина—Уотсона содержит зону неопределенности для значений статистики d. Другим преимуществом теста является возможность обобщения: в число регрессоров могут быть включены не только остатки с лагом 1, но и слагом 2, 3 и т д., что позволяет выявить корреляцию не только между соседними, но и между более отдаленными наблюдениями.

Вернемся к примеру зависимости курса ценной бумаги А от времени и применим тест серий Бреуша—Годфри.

Рассмотрим авторегрессионную зависимость остатков от их предьщущих значений, используя авторегрессионную модель р-го порядка AR{p). Применяя метод наименьших квадратов, получим следующее уравнение:

e =0,56 e -0,12е -0,01 e

(0,10) (0,12) (0,10)

Как видно, значимым оказывается только регрессор e т. е. существенное влияние на результат наблюдения e оказывает только одно предыдущее значение e Положительность оценки соответствующего коэффициента регрессии указывает на положительную корреляцию между ошибками регрессии e и e .

18. Понятие автокорреляции. Тесты на наличие автокорреляции. Тест Дарбина-Уотсона.

Автокорреляция- зависимость последующих уравнений ряда от предыдущих.

Тест Дарбина—Уотсона. Этот простой критерий (тест) определяет наличие автокорреляции между соседними членами.

Тест Дарбина—Уотсона основан на простой идее: если корреляция ошибок регрессии не равна нулю, то она присутствует и в остатках регрессии e , получающихся в результате применения обычного метода наименьших квадратов. В тесте Дарбина—Уотсона для оценки корреляции используется статистика вида

d=

Несложные вычисления позволяют проверить, что статистика Дарбина—Уотсона следующим образом связана с выборочным коэффициентом корреляции между соседними наблюдениями:

d=2(1-r)

В самом деле

(7.30)

d= = 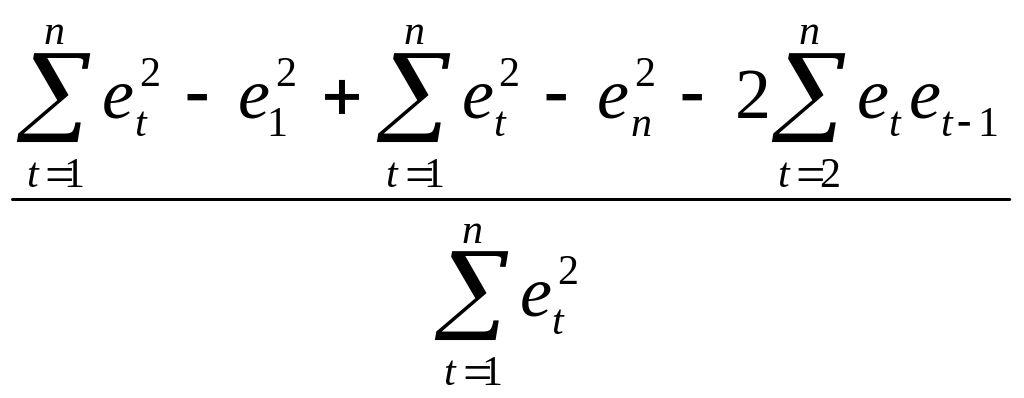=2*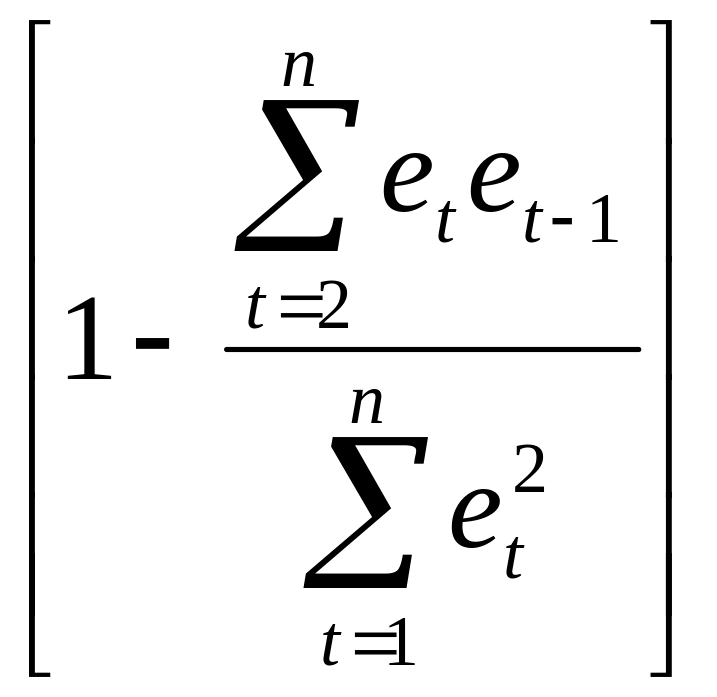 - 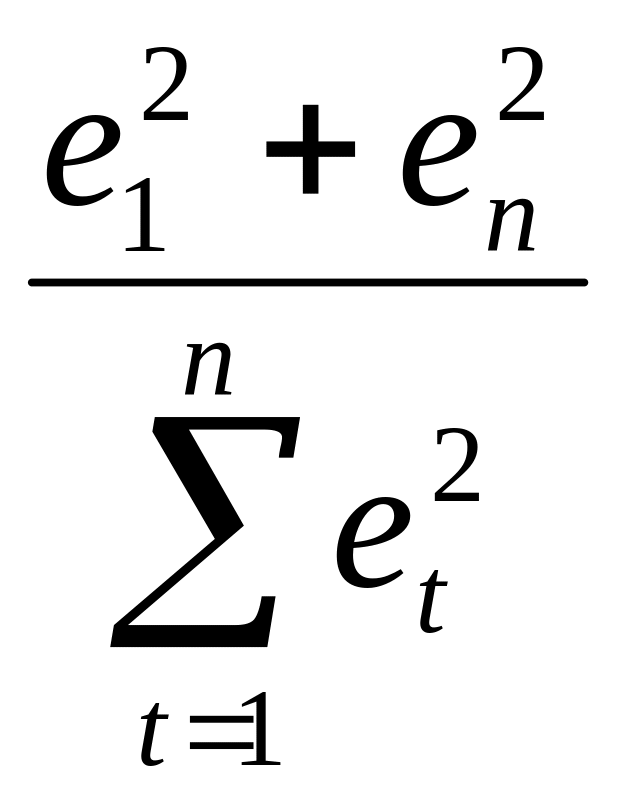При большом числе наблюдений n сумма e + значительно меньше и

d=2 ,

откуда и следует приближённое равенство (7.30), так как в силу условия =0

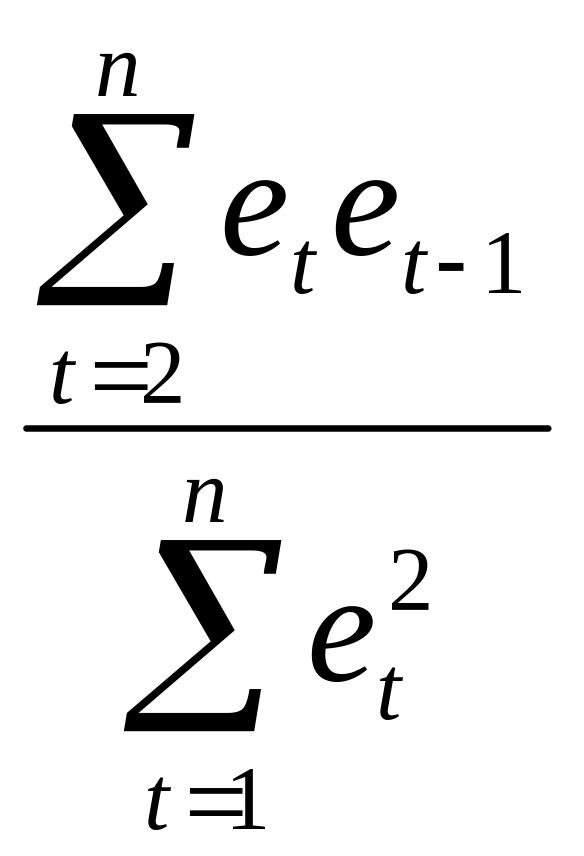=r.

Естественно, что в случае отсутствия автокорреляции выборочный коэффициент г окажется не сильно отличающимся от нуля, а значение статистики d будет близко к двум. Близость наблюдаемого значения к нулю должна означать наличие положительной автокорреляции, к четырем — отрицательной. Хотелось бы получить соответствующие пороговые значения, которые присутствуют в статистических критериях и либо позволяют принять гипотезу, либо заставляют ее отвергнуть (см. § 2.8). К сожалению, однако, такие пороговые (критические) значения однозначно указать невозможно.

Тест Дарбина—Уотсона имеет один существенный недостаток—распределение статистики d зависит не только от числа наблюдений, но и от значений регрессоров X (j= 1, ..., p). Это означает, что тест Дарбина—Уотсона, вообще говоря, не представляет собой статистический критерий, в том смысле, что нельзя указать критическую область, которая позволяла бы отвергнуть гипотезу об отсутствии корреляции, если бы оказалось, что в эту область попало наблюдаемое значение статистики d. Однако существуют два пороговых значения d и d , зависящие т о л ь к о от числа наблюдений, числа регрессоров и уровня значимости, такие, что выполняются следующие условия.

Если фактически наблюдаемое значение d: а) d < d < 4— d , то гипотеза об отсутствии автокорреляции

не отвергается (принимается); б) d < d < d или 4 — d < d < 4— d , то вопрос об отвержении

или принятии гипотезы остается открытым (область неопределенностикритерия) ;в) О < d < d , то принимается альтернативная гипотеза о положительной

автокорреляции;

г) 4— d < d < 4, то принимается альтернативная гипотеза об

отрицательной автокорреляции.

Изобразим результат Дарбина—Уотсона графически:

Для d-статистики найдены верхняя dви нижняя dн границы на уровнях значимости а = 0,01; 0,025 и 0,05. В табл. V приложений приведены значения статистик dв и dн критерия Дарбина—Уотсона на уровне значимости а = 0,05.

Недостатками критерия Дарбина—Уотсона является наличие области неопределенности критерия, а также то, что критические значения d-статистики определены для объемов выборки не менее 15. Тем не менее тест Дарбина—Уотсона является наиболее употребляемым.

19. Понятие гетероскедастичности остатков. Оценка параметров модели в случае гетероске-дастичности.Гетероскедастичность. При эконометрическом моделировании реальных экономических процессов предпосылки регрессионного анализа нередко оказываются нарушенными: дисперсии остатков модели не одинаковы (гетероскедастичность остатков). В этом случае оценки параметров уравнения регрессии, полученные методом наименьших квадратов, будут не эффективными. Проверить модель на гетероскедастичность можно с помощью следующих тестов: ранговой корреляции Спирмена; Голдфельда-Квандта; Уайта; Глейзера. Рассмотрим тест на гетероскедастичность, применяемый в случае, если ошибки регрессии можно считать нормально распределенными случайными величинами, – тест Голдфелда-Квандта. Все n наблюдений упорядочиваются в порядке возрастания значений фактора X. Затем выбираются m первых и m последних наблюдений. Гипотеза о гомоскедастичности равносильна тому, что значения остатков e₁, e_m и e_n-m+1, e_n представляют собой выборочные наблюдения нормально распределенных случайных величин, имеющих одинаковые дисперсии. Гипотеза о равенстве дисперсий двух нормально распределенных совокупностей проверяется с помощью F-критерия Фишера. Расчетное значение вычисляется по формуле: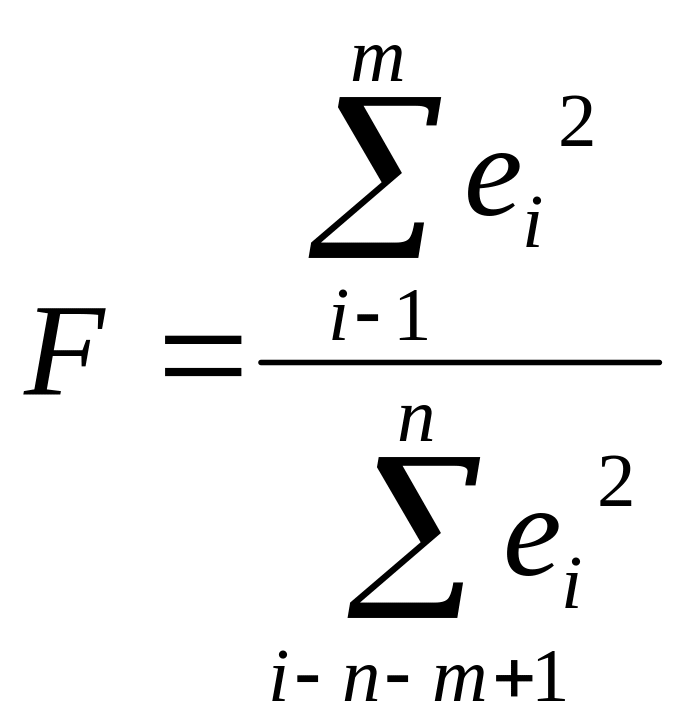 . Гипотеза о равенстве дисперсий двух наборов по m наблюдений (т.е. гипотеза об отсутствии гетероскедастичности остатков) отвергается, если расчетное значение превышает табличное F >F_α;m-p;m-p, где p – число регрессоров. Мощность теста максимальна, если выбирать m порядка n/3. Тест Голдфельда-Квандта позволяет выявить факт наличия гетероскедастичности, но не позволяет описать характер зависимостей дисперсий ошибок регрессии количественно. Рассмотрим наиболее простой и часто используемый тест Уайта. Предполагают, что дисперсии ошибок регрессии представляют собой одну и ту же функцию от наблюдаемых значений факторов, т.е.σ²_i =f(x_i), i = 1, …, n. Как правило, эту функцию выбирают квадратичной (в случае гомоскедастичности остатков f = const). Методом наименьших квадратов оценивают параметры уравнения регрессии для квадратов остатков:е²_i =f(x_i) + u_i, i = 1, …, n. В случае незначимости уравнения регрессии в целом принимается гипотеза об отсутствии гетероскедастичности. Наилучшим образом характер гетероскедастичности определяется при помощи теста Глейзера. Осуществляется регрессия: е²_i =f(x_i) + u_i, i = 1, …, n. В качестве функции f обычно выбирается функция видаf = a + х² Регрессия осуществляется при разных значениях , затем выбирается то значение, при котором коэффициент оказывается наиболее значимым, т.е. имеет наибольшее значение t-статистики. Этим уравнением и аппроксимируется гетероскедастичность. Устранение гетероскедастичности. Пусть модель гетероскедастична, т.е. дисперсии ошибок не равны между собой, а сами ошибки не коррелированы. Тогда имеем, что ковариационная матрица ошибок Ω – диагональная: 1) Пусть дисперсии ошибок известны. В соответствии с обобщенным методом наименьших квадратов переходим к нормированным по σ_i переменным: Z = Y/σ_i , V_j = X_j/σ_i , i = 1, …, n. В новых переменных модель примет вид:z_i = β^'₀ + + ν_i где β^'₀ = β₀/σ_i, ν_i = ε_i/σ_iДля новой модели дисперсия равна D(ν_i) = 1, т.е. модель гомоскедастична. В случае гетероскедастичности остатков метод наименьших квадратов называется взвешенным методом наименьших квадратов, поскольку каждое наблюдение «взвешивается» с помощью коэффициента 1/σ_i. На практике, однако, значения σ_i почти никогда не бывают известны. Поэтому сначала находят оценку вектора параметров обычным методом наименьших квадратов. Затем находят регрессию квадратов остатков на квадратичные функции объясняющих переменных, т.е. уравнение е²_i =f(x_i) + u_i, i = 1, …, n, где f(x_i) – квадратичная функция. Далее по полученному уравнению рассчитывают теоретические значения и определяют набор весов . Затем вводят новые переменные Y^*_i = Y/σ_i, X^*_j = X_j/σ_i, j = 1,…,m и находят уравнение . Полученная оценка и есть оценка взвешенного метода наименьших квадратов.

23. Неднородность данных в регрессионном смысле. Использование фиктивных переменных в регрессионных моделях. Интерпретация коэффциентов при фиктивных переменных.

При изучении социально-экономических процессов и явлений может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровня, например, образование, пол, фактор сезонности. Качественные признаки могут существенно влиять на структуру линейных связей между переменными и приводить к скачкообразному изменению параметров регрессионной модели. В этом случае говорят об исследовании регрессионных моделей с переменной структурой или построении регрессионных моделей по неоднородным данным.

Оценить влияние значений количественных переменных и уровней качественных признаков с помощью одного уравнения регрессии можно путем введения фиктивных переменных.

В качестве фиктивных переменных обычно используются дихотомические (бинарные) переменные, которые принимают всего два значения: «0» и «1». Например, при исследовании зависимости заработной платы от уровня образования Z можно рассмотреть k=3 уровня: начальное образование, среднее и высшее. Обычно вводят (k-1) бинарную переменную. В нашем случае потребуется ввести две фиктивные переменные.

Тогда регрессионная модель запишется в виде:

y= b₀ + b₁∙x₁ + … + b_m∙x_m + b_m+1∙z₁ + b_m+2∙z₂ +ε,

где

x₁, …,∙x_n – экономические (количественные) переменные.

Наличие у работника начального образования будет отражено парой значений z₁=0, z₂=0.

Параметры при фиктивных переменных z₁ и z₂ представляют собой разность между средним уровнем результативного признака для соответствующей группы и базовой группы (в нашем примере это работники с начальным образованием).

При построении регрессионных моделей по неоднородным данным необходимо выяснить, действительно ли две выборки однородны в регрессионном смысле, можно ли объединить их в одну и рассматривать единую модель регрессии?

Для ответа на этот вопрос можно воспользоваться тестом Г.Чоу.

По каждой выборке строятся две линейные регрессионные модели:

Проверяемая нулевая гипотеза имеет вид – H₀: b'=b''; D(ε')= D(ε'')= σ².

Если нулевая гипотеза верна, то две регрессионные модели можно объединить в одну объема n = n₁ + n₂.

Согласно критерию Г.Чоу нулевая гипотеза H₀ отвергается на уровне значимости α, если статистика

где 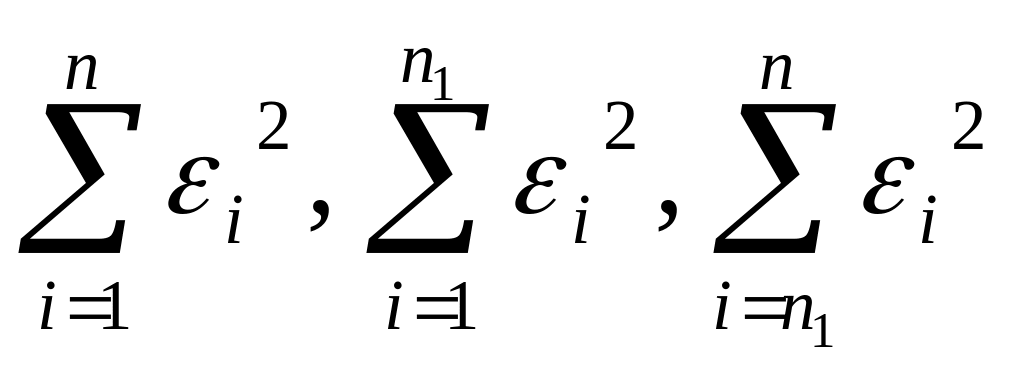- остаточные суммы квадратов соответственно для объединенной, первой и второй выборок, n = n₁ + n₂.

Для проверки гипотезы о структурной стабильности тенденции изучаемого временного ряда можно использовать тест Д.Гуйарати.

Пример 4. Рассмотрим полученную в примере 1 модель зависимости балансовой прибыли предприятия торговли  (тыс. руб.) от следующих переменных:

- фонд оплаты труда, тыс. руб.; - объем продаж по безналичному расчету, тыс. руб.

Известно, что первая выборка значений переменных объемом n₁=12 получена при одних условиях, а другая, объемом n₂=12, - при несколько измененных условиях.