Вопрос 8.

Парадо́кс дней рожде́ния — кажущееся парадоксальным утверждение, что вероятность совпадения дней рождения (числа и месяца) хотя бы у двух членов группы из 23 и более человек превышает 50 %. Для 60 и более человек вероятность такого совпадения превышает 99 %, хотя 100 % она достигает только когда в группе не менее 367 человек (с учётом високосных лет).

Расчтёт вероятности.

В данном примере для расчёта вероятности того, что в группе из n человек как минимум у двух дни рождения совпадут, примем, что дни рождения распределены равномерно, то есть нет високосных лет, близнецов, рождаемость не зависит от дня недели, времени года и других факторов. В действительности, это не совсем так — обычно летом рождается больше детей; кроме того, в некоторых странах из-за особенностей работы больниц больше детей рождается в определённые дни недели. Однако неравномерность распределения может лишь увеличить вероятность совпадения дней рождения, но не уменьшить: если бы все люди рождались только в 3 дня из 365, то вероятность совпадения дней рождения была бы очень высокой.

Рассчитаем сначала, какова вероятность p (n) того, что в группе из n человек дни рождения всех людей будут различными. Если n > 365, то в силу принципа Дирихле вероятность равна нулю. Если же n ≤ 365, то будем рассуждать следующим образом. Возьмём наугад одного человека из группы и запомним его день рождения. Затем возьмём наугад второго человека, при этом вероятность того, что у него день рождения не совпадёт с днем рождения первого человека, равна 1 — 1/365. Затем возьмём третьего человека, при этом вероятность того, что его день рождения не совпадёт с днями рождения первых двух, равна 1 — 2/365. Рассуждая по аналогии, мы дойдём до последнего человека, для которого вероятность несовпадения его дня рождения со всеми предыдущими будет равна 1 — (n — 1)/365. Перемножая все эти вероятности, получаем вероятность того, что все дни рождения в группе будут различными:

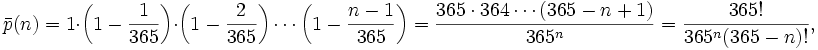
Тогда вероятность того, что хотя бы у двух человек из n дни рождения совпадут, равна

Значение этой функции превосходит 1/2 при n = 23. При этом вероятность совпадения равна примерно 50.7 %

Вопрос 9.

Асимметричное шифрование

— система шифрования и/или электронной цифровой подписи, при которой открытый ключ передаётся по открытому каналу, и используется для проверки ЭЦП и для шифрования сообщения. Для генерации ЭЦП и для расшифровки сообщения используется секретный ключ. Криптографические системы с открытым ключом в настоящее время широко применяются в различных сетевых протоколах, в частности, в протоколах TLS и его предшественнике SSL (лежащих в основе HTTPS), в SSH. Также используется в PGP, S/MIME.

Основная идея.

очень тесно связана с идеей односторонних функций, то есть таких функций f(x), что по известному x довольно просто найти значениеf(x), тогда как определение x из f(x) невозможно за разумный срок.

Но сама односторонняя функция бесполезна в применении: ею можно зашифровать сообщение, но расшифровать нельзя. Поэтому криптография с открытым ключом использует односторонние функции с лазейкой. Лазейка — это некий секрет, который помогает расшифровать. То есть существует такой y, что зная f(x) и y, можно вычислить x.

Схема шифрования.

Пусть K — пространство ключей, а e и d — ключи шифрования и расшифрования соответственно. E_e — функция шифрования для произвольного ключа e K, такая что:

E_e(m) = c

Здесь c C, где C — пространство шифротекстов, а m M, где M — пространство сообщений.

D_d — функция расшифрования, с помощью которой можно найти исходное сообщение m, зная шифротекст c :

D_d(c) = m

{E_e: e K} — набор шифрования, а {D_d: d K} — соответствующий набор для расшифрования. Каждая пара (E,D) имеет свойство: зная E_e, невозможно решить уравнение E_e(m) =c, то есть для данного произвольного шифротекста c C, невозможно найти сообщение m M. Это значит, что по данному e невозможно определить соответствующий ключ расшифрования d. E_e является односторонней функцией, а d — лазейкой.^[3]

Ниже показана схема передачи информации лицом А лицу В. Они могут быть как физическими лицами, так и организациями и так далее. Но для более лёгкого восприятия принято участников передачи отождествлять с людьми, чаще всего именуемыми Алиса и Боб. Участника, который стремится перехватить и расшифровать сообщения Алисы и Боба, чаще всего называют Евой.

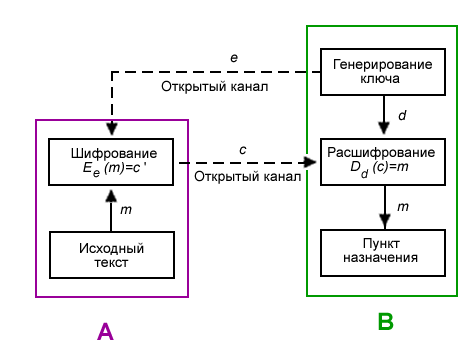
1. Боб выбирает пару (e,d) и шлёт ключ шифрования e (открытый ключ) Алисе по открытому каналу, а ключ расшифрования d (закрытый ключ) защищён и секретен (он не должен передаваться по открытому каналу).

2. Чтобы послать сообщение m Бобу, Алиса применяет функцию шифрования, определённую открытым ключом e: E_e(m) = c, c — полученный шифротекст.

3. Боб расшифровывает шифротекст c, применяя обратное преобразование D_d, однозначно определённое значением d.

Принципы построения.

1. Начинаем с трудной задачи P. Она должна решаться сложно в смысле теории: не должно быть алгоритма, с помощью которого можно было бы перебрать все варианты решения задачи P за полиномиальное время относительно размера задачи. Более правильно сказать: не должно быть известного полиномиального алгоритма, решающего данную задачу — так как ни для одной задачи ещё пока не доказано, что для неё подходящего алгоритма нет в принципе.

2. Можно выделить легкую подзадачу P' из P. Она должна решаться за полиномиальное время, лучше, если за линейное.

3. «Перетасовываем и взбалтываем» P', чтобы получить задачу P'', совершенно не похожую на первоначальную. Задача P'', по крайней мере, должна выглядеть как оригинальная труднорешаемая задача P.

4. P'' открывается с описанием, как она может быть использована в роли ключа зашифрования. Как из P'' получить P', держится в секрете как секретная лазейка.

5. Криптосистема организована так, что алгоритмы расшифрования для легального пользователя и криптоаналитика существенно различны. В то время как второй решаетP'' задачу, первый использует секретную лазейку и решает P' задачу.