
- •Вопрос 1.
- •Вопрос 2.
- •Вопрос 3.
- •Формальное описание
- •Комментарии к алгоритму.
- •Вопрос 4.
- •Умножение и факторизация
- •Возведение в квадрат и извлечение квадратного корня по модулю
- •Дискретное экспоненцирование и логарифмирование
- •Криптографические хэш-функции
- •Другие претенденты
- •Вопрос 6.
- •1. Заполнение памяти.
- •2. Определение ключа.
- •Вопрос 7.
- •Вопрос 8.
- •Вопрос 9.
- •Применение.
- •Преимущества
- •Недостатки.
- •Вопрос 10.
- •Вопрос 11.
- •Обеспечение целостности данных с использование шифрации и mac
- •Вопрос 12.
- •Использование хеш-функций
- •Симметричная схема
- •Асимметричная схема
- •Пример алгоритмов.
- •Модели атак и их возможные результаты.
- •Вопрос 13.
- •Вопрос 14.
- •Вопрос 15.
- •Вопрос 16.
Вопрос 2.
Модульная арифметика.
Группа.
Непустое
множество G с
заданной на нём бинарной
операцией ![]() называется
группой (G,
* ), если выполнены следующие аксиомы:
называется
группой (G,
* ), если выполнены следующие аксиомы:
ассоциативность:
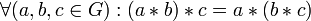 ;
;наличие нейтрального элемента:
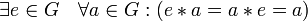 ;
;наличие обратного элемента:

Простейшие свойства.
Обратный к данному элемент всегда определяется однозначно.
(a−1)-1 = a, aman = am+n, (am)n = amn.
(ab)−1 = b−1a−1.
Верны законы сокращения:
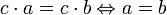 ,
,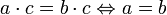 .
.
Обратный элемент к нейтральному есть сам нейтральный элемент.
Группа содержит единственное решение x любого уравнения x · c = b или c · x = b; то есть в группе возможны однозначно определённые правое и левое «деление».
Пересечение двух подгрупп группы G есть подгруппа группы G.
Группы Z+p , Z*p.
Алгоритм Евклида.
Пусть a и b — целые числа, не равные одновременно нулю, и последовательность чисел
![]()
определена тем, что каждое rk — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть
a = bq0 + r1
b = r1q1 + r2
r1 = r2q2 + r3
![]()
rk − 2 = rk − 1qk − 1 + rk
rn − 1 = rnqn
Тогда НОД(a,b), наибольший общий делитель a и b, равен rn, последнему ненулевому члену этой последовательности.
Существование таких r1,r2,...,
то есть возможность деления с
остатком m на n для
любого целого m и
целого ![]() ,
доказывается индукцией по m.
,
доказывается индукцией по m.
Корректность
этого алгоритма вытекает из следующих двух утверждений:
Пусть a = bq + r, тогда НОД (a,b) = НОД (b,r).
Доказательство .
Пусть k — любой общий делитель чисел a и b, не обязательно максимальный, тогда a = t1 * k ; b = t2 * k; где t1 и t2 — целые числа из определения.
Тогда k также общий делитель чисел b и r, так как b делится на k по определению, а r = a − bq = (t1 − t2 * q) * k (выражение в скобках есть целое число, следовательно, k делит r без остатка)
Обратное также верно и доказывается аналогично пункту 2 - любой делитель b и r так же является делителем a и b.
Следовательно, все общие делители пар чисел a,b и b,r совпадают. Другими словами, нет общего делителя у чисел a,b, который не был бы также делителем b,r, и наоборот.
В частности, максимальный делитель остается тем же самым. Что и требовалось доказать.
НОД (0,r) = r для любого ненулевого r.
Проще сформулировать алгоритм Евклида так: если даны натуральные числа a и b и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.
Китайская теорема об остатках.
Если натуральные
числа ![]() попарно
взаимно просты,
то для любых целых
попарно
взаимно просты,
то для любых целых ![]() таких,
что
таких,
что ![]() при
всех
при
всех ![]() ,
найдётся число N,
которое при делении на ai даёт
остаток ri при
всех
.
Более того, если найдутся два таких
числа N1и N2,
то
,
найдётся число N,
которое при делении на ai даёт
остаток ri при
всех
.
Более того, если найдутся два таких
числа N1и N2,
то ![]() .
.
Вопрос 3.
Квадратичный вычeт.
Квадратичный
вычет по
модулю m — целое
число a,
для которого разрешимо сравнение![]()
Если указанное сравнение не разрешимо, то число a называется квадратичным невычетом по модулю m.
Свойства.
Критерий Эйлера: Пусть p > 2 простое.Число a, взаимно простое с p, является квадратичным вычетом по модулю p тогда и только тогда, когда
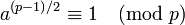 и является квадратичным невычетом по
модулю p тогда
и только тогда, когда
и является квадратичным невычетом по
модулю p тогда
и только тогда, когда
Квадратичный закон взаимности
Квадратичные вычеты, взаимно простые с модулем, образуют мультипликативную подгруппу кольца вычетов, в частности:
вычет ![]() вычет
= вычет;
вычет
= вычет;
невычет вычет= невычет.
Символ Лежандра.
Пусть a —
целое число, и p —
нечётное простое
число.
Символ Лежандра ![]() определяется
следующим образом:
определяется
следующим образом:
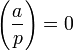 ,
если a делится
на p.
,
если a делится
на p.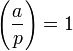 ,
если a является квадратичным
вычетом по
модулю p
,
если a является квадратичным
вычетом по
модулю p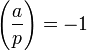 ,
если a является квадратичным
невычетом по
модулю p
,
если a является квадратичным
невычетом по
модулю p
Свойства.
Мультипликативность:
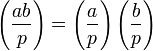 .
.Если
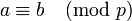 ,
то
,
то  .
.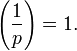
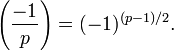
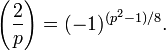
Если q — простое число, не равное p, то
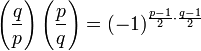 —
частный случай квадратичного
закона взаимности.
—
частный случай квадратичного
закона взаимности.Среди чисел
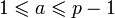 ровно
половина имеет символ Лежандра, равный
+1, а другая половина — −1.
ровно
половина имеет символ Лежандра, равный
+1, а другая половина — −1.Символ Лежандра при p > 2 можно вычислить по формуле Эйлера:
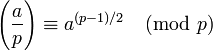 .
.
Символ Якоби.
Пусть P — нечётное,
большее единицы число и ![]() —
его разложение на простые множители
(среди
—
его разложение на простые множители
(среди ![]() могут
быть равные). Тогда для
произвольного целого числа a символ
Якоби определяется равенством:
могут
быть равные). Тогда для
произвольного целого числа a символ
Якоби определяется равенством:
![]() где
где ![]() — символы
Лежандра.
По определению считаем, что
— символы
Лежандра.
По определению считаем, что ![]() для
всех a.
для
всех a.
Свойства.
Мультипликативность:
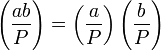 .
.В частности,
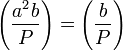 .
.Периодичность: если
 ,
то
,
то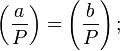
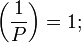
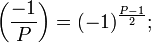
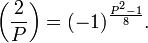
Если Q — нечётное натуральное число, взаимно простое с P, то
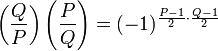 —
аналог квадратичного
закона взаимности.
—
аналог квадратичного
закона взаимности.В частности, если P и Q взаимно простые и нечётные, то
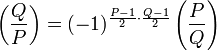 .
.Символ Якоби
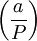 равен знаку
перестановки приведённой
системы вычетов по
модулю P,
которая задаётся как умножение элементов
этой группы на a (где обязательно
взаимно просто с P).
равен знаку
перестановки приведённой
системы вычетов по
модулю P,
которая задаётся как умножение элементов
этой группы на a (где обязательно
взаимно просто с P).
Применение.
Главным образом, символ Якоби используется для быстрого вычисления символа Лежандра.
Символ
Лежандра, в свою очередь, необходим для
проверки разрешимости квадратичного
сравнения по модулю простого числа. Но
считать его по определению (то есть
вычислять ![]() ) —
достаточно долгая по времени процедура.
С помощью алгоритма быстрого
возведения в степень это
делается за O(log3p) битовых
операций (если не использовать быстрое
умножение и деление). А вычисление
символа Якоби требует только O(log2p) битовых
операций.
) —
достаточно долгая по времени процедура.
С помощью алгоритма быстрого
возведения в степень это
делается за O(log3p) битовых
операций (если не использовать быстрое
умножение и деление). А вычисление
символа Якоби требует только O(log2p) битовых
операций.
Символ Якоби используется в некоторых тестах на простоту, например, в (N+1)-методах и, как уже было сказано, в тесте Соловея — Штрассена.
Алгоритм.
