- •Вопрос 1.
- •Вопрос 2.
- •Вопрос 3.
- •Формальное описание
- •Комментарии к алгоритму.
- •Вопрос 4.
- •Умножение и факторизация
- •Возведение в квадрат и извлечение квадратного корня по модулю
- •Дискретное экспоненцирование и логарифмирование
- •Криптографические хэш-функции
- •Другие претенденты
- •Вопрос 6.
- •1. Заполнение памяти.
- •2. Определение ключа.
- •Вопрос 7.
- •Вопрос 8.
- •Вопрос 9.
- •Применение.
- •Преимущества
- •Недостатки.
- •Вопрос 10.
- •Вопрос 11.
- •Обеспечение целостности данных с использование шифрации и mac
- •Вопрос 12.
- •Использование хеш-функций
- •Симметричная схема
- •Асимметричная схема
- •Пример алгоритмов.
- •Модели атак и их возможные результаты.
- •Вопрос 13.
- •Вопрос 14.
- •Вопрос 15.
- •Вопрос 16.
Вопрос 1.
Криптогра́фия
— наука о методах обеспечения конфиденциальности (невозможности прочтения информации посторонним) и аутентичности (целостности и подлинности авторства, а также невозможности отказа от авторства) информации.
Сложность.
В информатике, теория сложности вычислений является разделом теории вычислений, изучающим стоимость работы, требуемой для решения вычислительной проблемы. Стоимость обычно измеряется абстрактными понятиями времени и пространства, называемыми вычислительными ресурсами. Время определяется количеством элементарных шагов, необходимых для решения проблемы, тогда как пространство определяется объёмом памяти или места на носителе данных.
Классы сложности P,BPP,NP.
Класс P.
В теории алгоритмов классом P (от англ. polynomial) называют множество задач, для которых существуют «быстрые» алгоритмы решения (время работы которых полиномиально зависит от размера входных данных).
Формальное определение.
Алгоритм
отождествляется с детерминированной
машиной Тьюринга,
которая вычисляет ответ по данному на
входную ленту слову из входного
алфавита Σ.
Временем работы алгоритма TM(x) при
фиксированном входном слове x называется
количество рабочих тактов машины
Тьюринга от начала до остановки машины.
Сложностью функции ![]() ,
вычисляемой некоторой машиной Тьюринга,
называется функция
,
вычисляемой некоторой машиной Тьюринга,
называется функция ![]() ,
зависящая от длины входного слова и
равная максимуму времени работы машины
по всем входным словам фиксированной
длины:
,
зависящая от длины входного слова и
равная максимуму времени работы машины
по всем входным словам фиксированной
длины:
![]() .
.
Если для функции f существует машина Тьюринга M такая, что CM(n) < nc для некоторого числа c и достаточно больших n, то говорят, что она принадлежит классу P, или полиномиальна по времени.
Класс BPP.
В теории алгоритмов классом сложности BPP (от англ. bounded-error, probabilistic, polynomial) называется класс предикатов, быстро (за полиномиальное время) вычислимых и дающих ответ с высокой вероятностью (причём, жертвуя временем, можно добиться сколь угодно высокой точности ответа). Задачи, решаемые вероятностными методами и лежащие в BPP, возникают на практике очень часто.
Формальное определение.
Классом BPP называется класс предикатов P(x), вычислимых на вероятностных машинах Тьюринга (обычных машинах Тьюринга с лентой случайных чисел) за полиномиальное время с ошибкой не более ⅓. Это значит, что вычисляющая значение предиката вероятностная машина Тьюринга даст ответ за время, равное O(nk), где n — длина x, причём если правильный ответ 1, то машина выдаёт 1 с вероятностью как минимум ⅔, и наоборот. Множество слов, на которых P(x) возвращает 1, называется языком, распознаваемым предикатом P(x).
Число
⅓ в определении выбрано произвольно:
если вместо него выбрать любое число p,
строго меньшее ½, то получится тот же
самый класс. Это верно, поскольку если
есть машина Тьюринга, распознающая язык
с вероятностью ошибки p за
время O(nk),
то точность можно сколь угодно хорошо
улучшить за счёт относительно небольшого
прироста времени. Если мы запустим
машину n раз
подряд, а в качестве результата возьмём
результат большинства запусков, то
вероятность ошибки упадёт до ![]() ,
а время станет равным O(nk+1).
Здесь n запусков
машины рассматриваются как схема
Бернулли с n испытаниями
и вероятностью успеха 1-p,
а формула, выражающая ошибку, — вероятность
неудачи не менее чем в половине случаев.
Если теперь запустить машину n2 раз
подряд, то время возрастёт до O(nk+2),
а вероятность ошибки упадёт до
,
а время станет равным O(nk+1).
Здесь n запусков
машины рассматриваются как схема
Бернулли с n испытаниями
и вероятностью успеха 1-p,
а формула, выражающая ошибку, — вероятность
неудачи не менее чем в половине случаев.
Если теперь запустить машину n2 раз
подряд, то время возрастёт до O(nk+2),
а вероятность ошибки упадёт до ![]() .
Таким образом, с ростом показателя
многочлена, оценивающего время, точность
растёт экспоненциально,
и можно достичь любого нужного значения.
.
Таким образом, с ростом показателя
многочлена, оценивающего время, точность
растёт экспоненциально,
и можно достичь любого нужного значения.
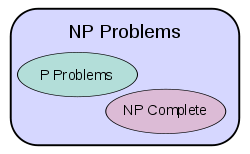
Класс NP.
В теории алгоритмов классом NP (от англ. non-deterministic polynomial) называют множество задач распознавания (англ.), решение которых при наличии некоторых дополнительных сведений (так называемого сертификата решения) можно «быстро» (за время, не превосходящее полинома от размера данных) проверить на машине Тьюринга.
Эквивалентно класс NP можно определить как содержащий задачи, которые можно «быстро» решить на недетерминированной машине Тьюринга.
Формальное определение.
(используя понятие недетерминированной машины Тьюринга, т. е. такой машины Тьюринга, у программы которой могут существовать разные строки с одинаковой левой частью) Если машина встретила «развилку», т. е. неоднозначность в программе, то дальше возможны разные варианты вычисления. Предикат R(x), который представляет данная недетерминированная машина Тьюринга, считается равным единице, если существует хоть один вариант вычисления, возвращающий 1, и нулю, если все варианты возвращают 0. Если длина вычисления, дающего 1, не превосходит некоторого многочлена от длины x, то предикат называется принадлежащим классу NP. Если у языка существует распознающий его предикат из класса NP, то язык называется принадлежащим классу NP. Это определение эквивалентно приведённому выше: в качестве свидетеля можно взять номера нужных веток при развилках в вычислении. Так как для x принадлежащему языку длина всего пути вычисления не превосходит многочлена от длины x, то и длина свидетеля также будет ограничена многочленом от длины x.
Всякую задачу о принадлежности слова x языку L, лежащую в классе NP, можно решить за экспоненциальное время перебором всех возможных сертификатов длины меньше| x | c.
Гипотеза P != NP.
В конечном счете проблема P = NP состоит в следующем: если положительный ответ на какой-то вопрос можно быстро проверить (за полиномиальное время), то правда ли, что ответ на этот вопрос можно быстро найти (за полиномиальное время и используя полиномиальную память)?
Неформально говоря, действительно ли решение задачи легче проверить, нежели отыскать?
Из
определения классов P и NP сразу
вытекает следствие: ![]() .
Однако до сих пор ничего не известно о
строгости этого включения, т. е.
существует ли задача, лежащая в NP,
но не лежащая в P.
Если такой задачи не существует, то все
задачи, принадлежащие классу NP,
можно будет решать за полиномиальное
время, что сулит огромную выгоду с
вычислительной точки зрения. Сейчас
самые сложные задачи из класса NP (так
называемые NP-полные
задачи)
можно решить за экспоненциальное время,
что почти всегда неприемлемо.
.
Однако до сих пор ничего не известно о
строгости этого включения, т. е.
существует ли задача, лежащая в NP,
но не лежащая в P.
Если такой задачи не существует, то все
задачи, принадлежащие классу NP,
можно будет решать за полиномиальное
время, что сулит огромную выгоду с
вычислительной точки зрения. Сейчас
самые сложные задачи из класса NP (так
называемые NP-полные
задачи)
можно решить за экспоненциальное время,
что почти всегда неприемлемо.