23. Колебательный контур

Электрические колебания могут возникать в цепи, содержащей индуктивность и емкость. Такая цепь называется к о л е б а т е л ь н ы м к о н т у р о м. На рис. 26.2,а изображены последовательные стадии колебательного процесса в идеализированном контуре с активным сопротивлением, равным нулю.

Д ля того чтобы вызвать колебания, можно присоединить отключенный от

называемого также импедансом цепи. Сопротивление R называют активнымсопротивлением (на нем выделяется тепло). Чисто мнимые сопротивления ωL и   называют соответственноиндуктивным и емкостным реактивными сопротивлениями (на них тепло не выделяется).

Напряжение на сопротивлении R:

,

 .

Напряжение на конденсаторе С:

,

.

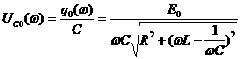Напряжение на катушке индуктивности L:

,

.

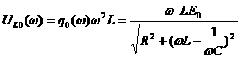Сравнивая написанные формулы, видим, что изменение напряжения на сопротивлении следует за изменением силы тока в цепи без отставания или опережения по фазе, изменение напряжение на конденсаторе отстает по фазе на  , а на индуктивности опережает по фазе на   изменение тока. Наглядно это можно изобразить с

или

где Е₀ - амплитуда переменной ЭДС; ω – ее циклическая частота.

Интересующее нас частное решение этого дифференциального уравнения имеет вид:

где

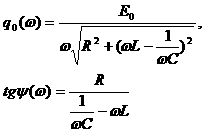
Решение соответствующего однородного уравнения, как мы видели в п.5.2, представляет собой свободные затухающие колебания, которые с течением времени становятся исчезающе малыми, и их можно в дальнейшем не учитывать.

Выпишем формулы для силы тока в цепи и падений напряжений на каждом из элементов контура.

Сила тока:  ,

 .

По аналогии с законом Ома для полной цепи по постоянному току величину

индуктивности конденсатор к источнику тока, вследствие чего на обкладках возникнут разноименные заряды величины q_m (стадия 1). Между обкладками возникнет электрическое поле, энергия которого равна

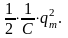
Если затем отключить источник тока и замкнуть конденсатор на индуктивность, емкость начнет разряжаться и в контуре потечет ток. В результате энергия электрического поля будет уменьшаться, но зато возникнет все возрастающая энергия магнитного поля, обусловленного током, текущим через индуктивность. Эта энергия равна .

Рис.26.2. Стадии колебательного движения в контуре (а) и его сопоставление с колебаниями пружинного маятника (б).

Так как активное сопротивление цепи равно нулю, полная энергия, слагающаяся из энергии электрического поля 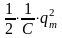и энергии магнитного поля , не расходуется на нагревание и будет оставаться постоянной. Поэтому в момент, когда напряжение на конденсаторе, а, следовательно, и энергия электрического поля обращаются в нуль, энергия магнитного поля, а значит, и ток достигают наибольшего значения (стадия 2; начиная с этого момента ток течет за счет ЭДС самоиндукции). В дальнейшем ток уменьшается и, когда заряды на обкладках достигнут первоначальной величины q_m, сила тока становится равной нулю (стадия 3). Затем те же процессы протекают в обратном порядке (стадии 4 и 5), после чего система приходит в первоначальное состояние (стадия 5) и весь цикл повторяется снова и снова. В ходе описанного процесса периодиче­ски изменяются (т. е. колеблются) заряд q на обкладках, напряжение U на конденсаторе и сила тока I, текущего через индуктивность. Колебания сопровождаются взаимными превращениями энергий электрического и магнитного полей.

На рис. 26.2,б колебаниям в контуре сопоставлены колебания пружинного маятника. Сообщению зарядов обкладкам конденсатора соответствует выведение маятника внешней силой из положения равновесия и сообщение ему первоначального отклонения х_м. При этом возникает потенциальная энергия упругой деформации пружины, равная . Стадии 2 соответствует прохождение маятника через положение равновесия. В этот момент квазиупругая сила равна нулю и маятник продолжает двигаться по инерции. К этому времени энергия маятника полностью переходит в кинетическую и определяется выражением . Сопоставление дальнейших стадий предоставляем читателю.

Из сопоставления электрических и механических колебаний следует, что энергия электрического поля аналогична потенциальной энергии упругой деформации, а энергия магнитного поля аналогична кинетической энергии. Индуктивность L играет роль массы m, величина, обратная емкости (1/С), - роль коэффициента жесткости k. Наконец, заряду q соответствует смещение маятника из положения равновесия х, а силе тока - скорость v. Как мы увидим ниже, аналогия между электрическими и механическими колебаниями распространяется и на описывающие их математические уравнения.

Во время колебаний внешнее напряжение к контуру не приложено. Поэтому падения напряжения на емкости и на индуктивности (вследствие явления самоиндукции) - в сумме должны дать нуль, т.к. Е = 0 в соответствующем уравнении Кирхгофа:

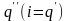Разделив это выражение на L и заменив через , придем к следующему уравнению:

Если ввести обозначение

уравнение (26.9) принимает вид

известный в теории колебаний как дифференциальное уравнение свободных (незатухающих) колебаний. Решение дифференциальных уравнений ищут в виде функции, которая, будучи подставлена в уравнение, после соответствующего дифференцирования, обращает уравнение в тождество. Решением уравнения (26.11) является функция

q = q_mcos(_ot + ). (26.12)

Таким образом, заряд на обкладках конденсатора изменяется по гармоническому закону с частотой, определяемой выражением (26.10). Эта частота называется собственной частотой контура (она соответствует собственной частоте гармонического осциллятора). Для периода колебаний получается так называемая формула Томсона:

Напряжение на конденсаторе отличается от заряда множителем 1/С:

Водород и углерод отличаются числом протонов в ядре и, следовательно, числом электронов в электронной оболочке. Число протонов в ядре атома называют зарядом ядра атома и обозначают буквой Z. Это очень важная величина. Когда мы перейдем к изучению Периодического закона, то увидим, что число протонов в ядре совпадает с порядковым номером атома в Периодической таблице Д.И.Менделеева.

Как мы уже говорили, заряд ядра (число протонов) совпадает с числом электронов в атоме. Когда атомы сближаются, то в первую очередь они взаимодействуют друг с другом не ядрами, а электронами. Число электронов определяет способность атома образовывать связи с другими атомами, то есть его химические свойства. Поэтому атомы с одинаковым зарядом ядра (и одинаковым числом электронов) ведут себя в химическом отношении практически одинаково и рассматриваются как атомы одного химического элемента.

ЭЛЕМЕНТОМ называется вещество, состоящее из атомов с одинаковым ЗАРЯДОМ ЯДРА.