2. Понятие смысл производной

Пусть функция определена на промежутке X. Возьмем точку и придадим этому значению некоторое приращение , такое, что новая точка . Тогда значение функции изменится до значения и приращение функции получиться

Если существует предел отношения приращения функции к вызвавшему его приращению независимой переменной , при стремлении к нулю, т.е.

то его называют производной функции по независимой переменной x в точке . В общем случае, когда производная находится в произвольной точке, аргумент можно не писать. Обозначается производная различными символами: .

Итак, производная функции , при условии существовании предела, определяется по формуле:

Дифференцирование функции- это операция нахождения производной функции.

Функция называется дифференцируемой в точке , если она имеет конечную производную в этой точке.

Функция называется дифференцируемой на промежутке , если она имеет конечную производную во всех точках этого промежутка.

Главный предмет дифференциального исчисления- вычисление производных, изучение и использование их свойств.

Вернемся к задачам, приводящим к понятию производной, рассмотренных ранее. Сравнивая определение и конкретное содержание задач, можно сформулировать механический, геометрический и экономический смысл производной.

Механический (физический) смысл производной: скорость v точки в момент времени есть производная пути s по времени t, т.е.

Геометрический смысл производной: угловой коэффициент касательной, проведенной к кривой в точке есть производная , т.е.

Используя геометрический смысл производной можно вывести уравнение касательной к некоторой кривой в данной точке. Из курса аналитической геометрии известно уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом: . Заменяя коэффициент k на производную , получим уравнение касательной к кривой в точке :

.

Кроме касательной существует еще одна прямая-нормаль к кривой, которая находит свое применение в приложениях.

Нормалью к кривой называется прямая, перпендикулярная касательной в точке касания. Из курса аналитической геометрии знаем, что если нормаль перпендикулярна касательной, значит, ее угловой коэффициент может быть определен по угловому коэффициенту касательной по формуле: . Заменяя коэффициент k на , получим уравнение нормали к кривой в точке :

.

Экономический смысл производной: производительность труда p в момент времени есть производная объема произведенной продукции V по времени t,т.е.

Рассмотрим, как связаны два важнейших свойства функции- непрерывность и дифференцируемость.

Теорема 5.1. Если функция дифференцируема в некоторой точке , то она и непрерывна в этой точке.

Доказательство. По условию теоремы, функция дифференцируема в точке , т.е. она имеет конечную производную, а именно существует предел:

, где конечна и не зависит от .

Используя третью запись предела, имеем:

где бесконечно малая функция.

Выразим (т.к. и при ).

Таким образом, . По определению непрерывности функция непрерывна в точке . Ч.Т.Д.

Обратное утверждение в общем случае неверно, т.е. если функция непрерывна в какой-то точке, то она не обязательно будет дифференцированной в этой точке. В качестве доказательства приведем пример.

Пример 5.1. Доказать, что функция не дифференцируема в точке .

Решение:

Рис.

По графику, представленному на рисунке видно, что функция непрерывна в точке 0.

………………………..

Таблица производных простых функций y=f(x)
Степенные функции	Показательные и логарифмические функции	Тригонометрические функции	Обратные тригонометрические функции
Таблица производных сложных функций y=f(u(x))
Степенные функции	Показательные и логарифмические функции	Тригонометрические функции	Обратные тригонометрические функции

Ex. 1. .

Решение. По формуле получим

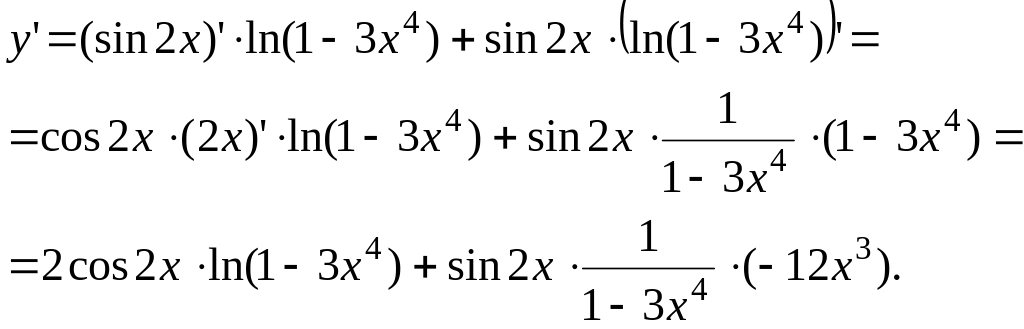
использовали правило дифференцирования сложной функции и таблицу производных.

Ex 2.

Решение.