2. Линейная зависимость и линейная независимость векторов Лекция 3.3 Аналитическая геометрия на плоскости и а пространстве

Время-2 а.ч.

План:

1. Метод координат на плоскости.

2. Виды уравнений прямой на плоскости.

3. Условие параллельности и перпендикулярности прямых на плоскости.

4. Прямая и плоскость в пространстве

Аналитическая геометрия- это раздел математики, который занимается исследованием геометрических фигур при помощи алгебраического анализа. В данном разделе всякий геометрический вопрос будет сведен к задаче вычисления.

Так как любая фигура является геометрическим местом точек, обладающим определенным свойством, то для ее изучения надо уметь определять с помощью чисел положение точки. Решение этой задачи стало возможным после создания Рене Декартом метода координат.

1. Метод координат на плоскости

Основанием аналитической геометрии служит метод координат.

Система координат на плоскости- способ, позволяющий численно описать положение точки плоскости.

Системы координат:

• в - числовая ось.

• в -декартовая система координат xOy; полярная система координат; косоугольная система координат; криволинейная система координат.

• В -декартовая система координат xyz; цилиндрическая система координат; сферическая система координат.

Мы рассмотрим две системы координат- декартовую и полярную.

Декартовая система координат (д.с.к.)	Полярная система координат (п.с.к.)
Задается двумя взаимно перпендикулярными прямыми- осями с выбранным направлением, масштабом и точкой отсчета. OX- ось абсцисс; OY- ось ординат.	Задается выходящим из полюса лучом (полярная ось) с масштабным отрезком. О- полюс; Op- полярная ось.
Координаты точки М в д.с.к. xOy-координаты радиус-вектора . Если , то координаты точки М(x;y), где x-абсцисса точки М, y- ордината точки М.	Координаты точки М в п.с.к. числа и , где -расстояние от точки М до полюса О, -угол, образованный отрезком ОМ с полярной осью (против часовой стрелки). , где -полярный радиус; - полярный угол.

Приложения метода координат на плоскости (расстояние между двумя точками, деление отрезка в данном отношении)

Расстояние между двумя точками

и

Деление отрезка в данном отношении

Разделим отрезок AB, где и в отношении .

Найдем координаты точки М(x;y):

- формулы деления отрезка в данном отношении.

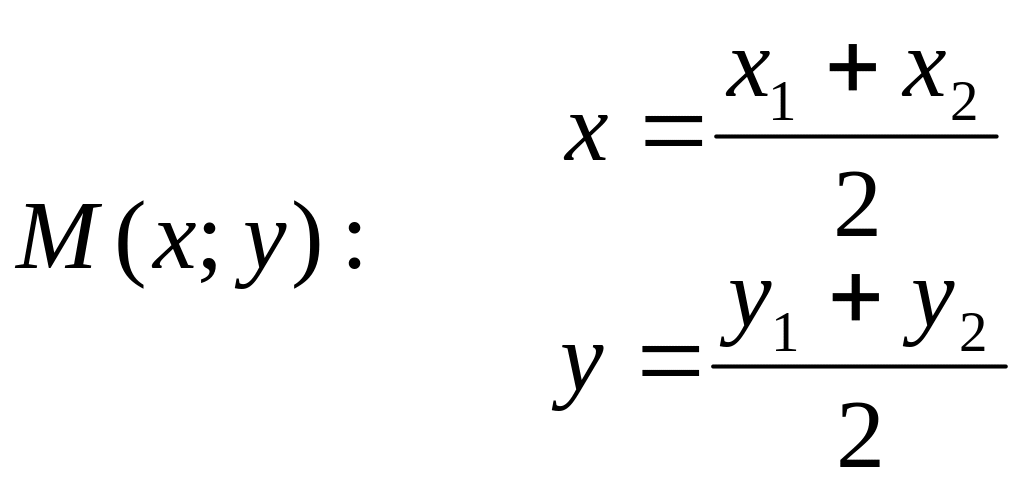- формулы деления отрезка пополам (M- середина отрезка AB).

2. Виды уравнений прямой на плоскости

Уравнение линии на плоскости –это уравнение . Простейшей линией на плоскости является прямая.

1. Общее уравнение прямой на плоскости- уравнение

, (3.7)

A, B, С- произвольные числа такие, что A и B не равны нулю одновременно.

Рассмотрим возможные частные случаи общего уравнения:

1) С=0

2)А=0

3) В=0

Получим из общего уравнения прямой другие наиболее важные виды.

2. Уравнение прямой в отрезках

Предположим, что в уравнении (3.7) все коэффициенты отличны от нуля. Проведем следующие преобразования:

Положим, . Тогда получим уравнение

,

называемое уравнением прямой в отрезках.

Коэффициенты a и b определяют отрезки на осях координат, отсекаемые данной прямой от начала координат:

Рис.

3. Уравнение прямой с угловым коэффициентом

Пусть уравнение (3.7) коэффициент . Выразим в этом уравнении y через x и получим

Положим, . Тогда получим уравнение

,

называемое уравнением прямой с угловым коэффициентом.

Угловой коэффициент равен тангенсу угла, образованного прямой с положительным направлением оси абсцисс, т.е. .

Рис.

4. Уравнение прямой, проходящей через данную точку в данном направлении.

Пусть прямая проходит через точку и ее направление характеризуется угловым коэффициентом k. Уравнение этой прямой можно записать в виде , где b-пока неизвестная величина. Так как прямая проходит через точку , то координаты точки удовлетворяют уравнению прямой: . Отсюда . Подставляя значение b в уравнение , получим искомое уравнение прямой , т.е.

,

называемое уравнением прямой проходящей через данную точку в данном направлении.

Данное уравнение с различными значениями называют также уравнением пучка прямых с центром в точке .

5. Уравнение прямой, проходящей через две точки.

Стр. 58 Присьменного